题目内容
曲线C:x2-y2=1的左支与直线y=kx+1只有一个公共点,则k的取值范围是 ________.
-1<k≤1,或k=
分析:先把直线与双曲线的方程联立消去y,可得方程,此方程有一个负根,先看k=1和-1时,k=-1符合题意,然后看-1<k<1时利用韦达定理求得x1x2的表达式,判断出结果消去0,可知-1<k<1符合,再看k<-1或k>1时利用△=0求得k的值,代入方程可知k= 时符合题意,之后综合答案可得.
时符合题意,之后综合答案可得.
解答:把直线与双曲线方程联立整理得
(1-k2)x2-2kx-2=0,③
③恰有一负根,
1)k=1时③变为-2x-2=0,x=-1;
2)k=-1时③变为2x-2=0,x=1(舍);
3)-1<k<1时x1x2=-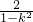 <0,③恰有一负根;
<0,③恰有一负根;
4)k<-1或k>1时
△=4k2+8(1-k2)=0,求得k=±
k= 时,x=-
时,x=- ;
;
k=- 时x=
时x= (舍).
(舍).
综上,-1<k≤1,或k= ,
,
故答案为:-1<k≤1,或k= ,
,
点评:本题主要考查了直线与圆锥曲线的关系.考查了学生分类讨论的思想的运用和分析问题,基本的运算能力.

分析:先把直线与双曲线的方程联立消去y,可得方程,此方程有一个负根,先看k=1和-1时,k=-1符合题意,然后看-1<k<1时利用韦达定理求得x1x2的表达式,判断出结果消去0,可知-1<k<1符合,再看k<-1或k>1时利用△=0求得k的值,代入方程可知k=
 时符合题意,之后综合答案可得.
时符合题意,之后综合答案可得.解答:把直线与双曲线方程联立整理得
(1-k2)x2-2kx-2=0,③
③恰有一负根,
1)k=1时③变为-2x-2=0,x=-1;
2)k=-1时③变为2x-2=0,x=1(舍);
3)-1<k<1时x1x2=-
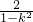 <0,③恰有一负根;
<0,③恰有一负根;4)k<-1或k>1时
△=4k2+8(1-k2)=0,求得k=±

k=
 时,x=-
时,x=- ;
;k=-
 时x=
时x= (舍).
(舍).综上,-1<k≤1,或k=
 ,
,故答案为:-1<k≤1,或k=
 ,
,点评:本题主要考查了直线与圆锥曲线的关系.考查了学生分类讨论的思想的运用和分析问题,基本的运算能力.

练习册系列答案
相关题目