题目内容

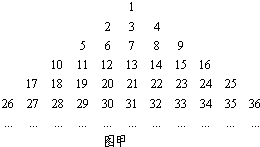 把正整数排列成如图甲三角形数阵,然后擦去第偶行数中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,设aij位于图乙三角形数表中从上往下数第i行第j列的数,若amn=2011,则实数对(m,n)为
把正整数排列成如图甲三角形数阵,然后擦去第偶行数中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,设aij位于图乙三角形数表中从上往下数第i行第j列的数,若amn=2011,则实数对(m,n)为分析:观察乙图,发现第k行有k个数,第k行最后的一个数为k2,前k行共有
个数,然后又因为442<2011<452,所以判断出这个数在第45行,而第45行的第一个数为1937,根据相邻两个数相差2,得到第45行38个数为2011,即可得到答案.
| k(k+1) |
| 2 |
解答:解:图乙中第k行有k个数,第k行最后的一个数为k2,前k行共有
个数,
由44×44=1936,45×45=2025知an=2011出现在第45行,第45行第一个数为1937,
第
+1=38个数为2011,
所以 实数对(m,n)为(45,38).
故答案为:(45,38)
| k(k+1) |
| 2 |
由44×44=1936,45×45=2025知an=2011出现在第45行,第45行第一个数为1937,
第
| 2011-1937 |
| 2 |
所以 实数对(m,n)为(45,38).
故答案为:(45,38)
点评:考查学生会根据图形归纳总结规律来解决问题,会进行数列的递推式运算,属中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目


 ,若
,若 则n=
。
则n=
。
 ,若
,若 ,则
,则 __________.
__________.