题目内容
如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为( )
A. | B. | C. | D. |
A
解析试题分析:该几何体为圆柱,底面半径为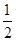 ,
,
所以几何体全面积为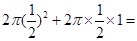
 ,故选A。
,故选A。
考点:本题主要考查三视图,几何体的全面积计算。
点评:简单题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。三视图视图过程中,要注意虚线的出现,意味着有被遮掩的棱。

练习册系列答案
相关题目
下面的图形可以构成正方体的是 ( )
| A. | B. | C. | D. |
将一些棱长为1的正方体放在 的平面上如图1所示,其正视图,侧视图如下所示.若摆放的正方体的个数的最大值和最小值分别为
的平面上如图1所示,其正视图,侧视图如下所示.若摆放的正方体的个数的最大值和最小值分别为 ,则
,则

| A.5 | B.6 | C.8 | D.9 |
点 在同一个球的球面,
在同一个球的球面, ,
,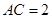 ,若四面体
,若四面体 体积的最大值为
体积的最大值为 ,则这个球的表面积为( )
,则这个球的表面积为( )
A. | B. | C. | D. |
如图,是一个几何体的正视图、侧视图、俯视图,且正视图、侧视图都是矩形,则该几何体的体积是
| A.24 | B.12 | C.8 | D.4 |
棱长为1的正方体ABCD-A1B1C1D1中,四面体AB1CD1的体积为( )
A. | B. | C.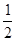 | D. |

 的正三角形,其俯视图是边长为2
的正三角形,其俯视图是边长为2




