题目内容
给出命题:①函数y=2sinx-cosx的值域是[-2,1];
②函数y=sinπxcosπx是周期为2的奇函数;
③
 是函数
是函数 的一条对称轴;
的一条对称轴;④若sin2α<0,cosα-sinα<0,则α一定为第二象限角;
⑤在△ABC中,若A>B则sinA>sinB.
其中正确命题的序号为 .
【答案】分析:利用辅助角公式,易将①中函数解析式化为正弦型函数的形式,进而判断①的真假;利用倍角公式,易将②中函数解析式化为正弦型函数的形式,进而判断②的真假;根据正弦函数的对称性,可以判断③的真假;根据倍角公式及三角函数在各象限中符号,我们易判断④的真假;由正弦定理的推论--边角互化,可以判断⑤的真假.进而得到结论.
解答:解:函数y=2sinx-cosx= sin(x+φ),则函数的值域为[-
sin(x+φ),则函数的值域为[- ,
,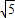 ],故①“函数y=2sinx-cosx的值域是[-2,1]”错误;
],故①“函数y=2sinx-cosx的值域是[-2,1]”错误;
函数y=sinπxcosπx= sin2πx,是周期为1的奇函数,故②“函数y=sinπxcosπx是周期为2的奇函数”错误;
sin2πx,是周期为1的奇函数,故②“函数y=sinπxcosπx是周期为2的奇函数”错误;
函数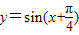 的对称轴是x=
的对称轴是x= +kπ,k∈Z,当k=-1时,
+kπ,k∈Z,当k=-1时, ,故③正确;
,故③正确;
若sin2α<0,则cosα与sinα异号,α可能为第II象限或第IV象限的角,又由cosα-sinα<0,则α一定是第II象限角,故④正确;
由正弦定理易得:在△ABC中,若A>B?sinA>sinB.故⑤正确
故答案为:③④⑤
点评:本题考查的知识是正弦型函数的值域、周期、对称性、三角函数的符号及正弦定理,是三角函数性质及应用的综合考查,但考查的面虽广,但难度不大,只要掌握正弦型函数的性质及其它相关的基本知识,即可解答,属基本题.
解答:解:函数y=2sinx-cosx=
 sin(x+φ),则函数的值域为[-
sin(x+φ),则函数的值域为[- ,
,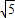 ],故①“函数y=2sinx-cosx的值域是[-2,1]”错误;
],故①“函数y=2sinx-cosx的值域是[-2,1]”错误;函数y=sinπxcosπx=
 sin2πx,是周期为1的奇函数,故②“函数y=sinπxcosπx是周期为2的奇函数”错误;
sin2πx,是周期为1的奇函数,故②“函数y=sinπxcosπx是周期为2的奇函数”错误;函数
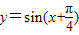 的对称轴是x=
的对称轴是x= +kπ,k∈Z,当k=-1时,
+kπ,k∈Z,当k=-1时, ,故③正确;
,故③正确;若sin2α<0,则cosα与sinα异号,α可能为第II象限或第IV象限的角,又由cosα-sinα<0,则α一定是第II象限角,故④正确;
由正弦定理易得:在△ABC中,若A>B?sinA>sinB.故⑤正确
故答案为:③④⑤
点评:本题考查的知识是正弦型函数的值域、周期、对称性、三角函数的符号及正弦定理,是三角函数性质及应用的综合考查,但考查的面虽广,但难度不大,只要掌握正弦型函数的性质及其它相关的基本知识,即可解答,属基本题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目