题目内容
设首项不为零的等差数列{an}前n项之和是Sn,若不等式an2+
≥λa12对任意{an}和正整数n恒成立,则实数λ的最大值为( )
| Sn2 |
| n2 |
| A、0 | ||
B、
| ||
C、
| ||
| D、1 |
分析:由等差数列{an}前n项之和是Sn,我们利用等差数列的前n项和公式,可将不等式an2+
≥λa12进行变形,配方后,根据实数的性质,易得实数λ的最大值.
| Sn2 |
| n2 |
解答:解:∵Sn=
n
∴an2+
≥λa12可以变形成:
an2+
a1an+(
-λ)a12≥0
即(
an+
a1)2+(
-λ)a12≥0
若不等式an2+
≥λa12对任意{an}和正整数n恒成立
仅需要λ≤
即可
则实数λ的最大值为
故选B
| (a1+an) |
| 2 |
∴an2+
| Sn2 |
| n2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
即(
| 5 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
若不等式an2+
| Sn2 |
| n2 |
仅需要λ≤
| 1 |
| 5 |
则实数λ的最大值为
| 1 |
| 5 |
故选B
点评:数列是一种定义域为正整数的特殊函数,我们可以利用研究函数的方式研究它,特别是等差数列对应的一次函数,等比数列对应的指数型函数,我们要善于通过数列的通项公式、前n项和公式,或数列相关的一些性质,在解数列相关的不等式时,也可以利用配方法、放缩法等解不等式的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
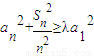 对任意an和正整数n恒成立,则实数λ的最大值为 .
对任意an和正整数n恒成立,则实数λ的最大值为 .