题目内容
一次数学考试中有A,B,C三道填空题为选做题,规定每个考生必须也只需选做其中的两道题,已知甲、乙两名考生都随机地选做了其中的两道题.
(I)求考生甲选做了A题的概率;
(II)求这三名学生中选做A题的人数ξ的分布列及期望Eξ.
(I)求考生甲选做了A题的概率;
(II)求这三名学生中选做A题的人数ξ的分布列及期望Eξ.
分析:(I)“考生甲选作了A题”事件包含:选作AB、AC两种情况,根据古典概型的概率计算公式即可求得;
(II)先求出A题被一生选中的概率及不被选中的概率,则三名学生选题相当于做了三次独立重复试验,由独立重复试验的概率计算公式可得ξ=0,1,2,3时的概率,进而得其分布列、期望;
(II)先求出A题被一生选中的概率及不被选中的概率,则三名学生选题相当于做了三次独立重复试验,由独立重复试验的概率计算公式可得ξ=0,1,2,3时的概率,进而得其分布列、期望;
解答:解:(Ⅰ)“考生甲选作了A题”事件包含:选作AB、AC两种情况,
所以考生甲选做A题的概率为:
=
;
(Ⅱ)显然ξ=0,1,2,3,由于A题不被甲选中的概率为
,被甲选中的概率为
,
所以P(ξ=0)=
(
)3=
,P(ξ=1)=
(
)2
=
,P(ξ=2)=
(
)(
)2=
,P(ξ=3)=
(
)3=
,
ξ的分布列如下所示:
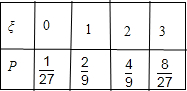
所以Eξ=0×
+1×
+2×
+3×
=2.
所以考生甲选做A题的概率为:
| ||||
|
| 2 |
| 3 |
(Ⅱ)显然ξ=0,1,2,3,由于A题不被甲选中的概率为
| 1 |
| 3 |
| 2 |
| 3 |
所以P(ξ=0)=
| C | 0 3 |
| 1 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
ξ的分布列如下所示:

所以Eξ=0×
| 1 |
| 27 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
| 27 |
点评:本题考查离散型随机变量的分布列、期望,独立重复试验,考查学生对问题的分析理解能力,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目