Question

【题目】已知函数f（x）=xlnx，g（x）= ．
（1）证明方程f（x）=g（x）在区间（1，2）内有且仅有唯一实根；
（2）记max{a，b}表示a，b两个数中的较大者，方程f（x）=g（x）在区间（1，2）内的实数根为x0 ， m（x）=max{f（x），g（x）}，若m（x）=n（n∈R）在（1，+∞）内有两个不等的实根x1 ， x2（x1＜x2），判断x1+x2与2x0的大小，并说明理由．

Answer 1

【答案】
（1）证明：令F（x）=f（x）﹣g（x），

则F（x）=xlnx﹣ ，定义域是（0，+∞），

F′（x）=1+lnx+ ，

x＞1时，F′（x）＞0，∴F（x）在（1，2）递增，

又F（1）=﹣ ＜0，F（2）=2ln2﹣ ＞0，

而F（x）在（1，+∞）上连续，

根据零点存在定理可得：F（x）=0在区间（1，2）有且只有1个实根，

即方程f（x）=g（x）在区间（1，2）内有且仅有唯一实根

（2）解：x1+x2＜2x0，

证明过程如下：

显然：m（x）= ，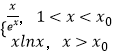

当1＜x＜x0时，m（x）= ，m′（x）= ＜0，

故m（x）单调递减；

当x＞x0时，m（x）=xlnx，m′（x）=1+lnx＞0，m（x）递增，

要证x1+x2＜2x0，

即证x2＜2x0﹣x1，

由（1）知x1＜x0＜x2，g（x1）=f（x2）=n，

故即证f（x2）＜f（2x0﹣x1），

即证g（x1）＜f（2x0﹣x1），

即证 ＜（2x0﹣x1）ln（2x0﹣x1），（1＜x1＜x0＜2），（*），

设H（x）= ﹣（2x0﹣x）ln（2x0﹣x），（1＜x＜x0＜2），

H′（x）= +ln（2x0﹣x）+1，

∵1＜x＜x0＜2，

∴ +1＞0，ln（2x0﹣x）＞0，

∴H′（x）＞0，

∴H（x）在（1，x0）递增，

即H（x）＜H（x0）=0，故（*）成立，

故x1+x2＜2x0成立

【解析】（1）求出函数的导数，通过解关于导函数的不等式，得到函数的单调性，结合零点存在定理证出结论即可；（2）问题转化为证 ＜（2x0﹣x1）ln（2x0﹣x1），（1＜x1＜x0＜2），（*），设H（x）= ﹣（2x0﹣x）ln（2x0﹣x），（1＜x＜x0＜2），根据函数的单调性证明即可．
【考点精析】通过灵活运用利用导数研究函数的单调性，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减即可以解答此题．