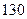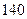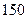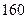题目内容
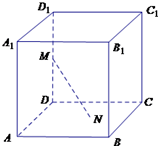
如图,在正方体ABCD-A1B1C1D1中,对角线A1C上一线段PQ=1,AB=2,则棱锥的体积VQ-PBD=______.
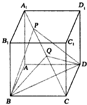

由题意知可以把P取到A点,这样的情况符合题意,
在三棱锥Q-ABD中,以△ABD为底面,
Q到上底面的距离是三棱锥的高,根据AQ=1,占对角线的
,
∴三棱锥的高是
×2=
,
∴棱锥的体积VQ-PBD=
×
×2×2×
=
,
故答案为:
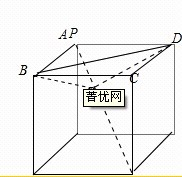
在三棱锥Q-ABD中,以△ABD为底面,
Q到上底面的距离是三棱锥的高,根据AQ=1,占对角线的
| 1 | ||
2
|
∴三棱锥的高是
| 1 | ||
2
|
| ||
| 3 |
∴棱锥的体积VQ-PBD=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 9 |
故答案为:
2
| ||
| 9 |


练习册系列答案
相关题目
 ,它的对角线的长
,它的对角线的长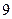 和
和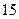 ,则这个棱柱的侧面积是( )
,则这个棱柱的侧面积是( )