题目内容
半径为1的球面上的四点A、B、C、D是正四面体的顶点，则A与B两点间的球面距离为 ．
【答案】分析：由题意将正四面体扩展为正方体求出正四面体的棱长，结合三角形利用余弦定理求出∠AOB，然后求出A与B两点间的球面距离即可．
解答：解：半径为1的球面上的四点A，B，C，D是正四面体的顶点，
所以正四面体扩展为正方体的外接球与圆柱球相同，
正方体的对角线就是外接球的直径，
所以正四面体的棱长为：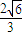
；
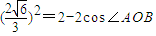
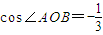
A与B两点间的球面距离为：
1×arccos（-
）=arccos（-
）=
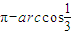
故答案为：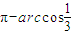
．
点评：本小题主要考查球面距离及相关计算等基础知识，考查运算求解能力，考查空间想象力．属于基础题．
解答：解：半径为1的球面上的四点A，B，C，D是正四面体的顶点，
所以正四面体扩展为正方体的外接球与圆柱球相同，
正方体的对角线就是外接球的直径，
所以正四面体的棱长为：
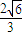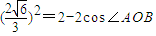
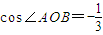
；A与B两点间的球面距离为：
1×arccos（-
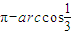
）=arccos（-）=故答案为：
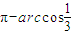．点评：本小题主要考查球面距离及相关计算等基础知识，考查运算求解能力，考查空间想象力．属于基础题．
练习册系列答案
相关题目
=0，
•
=0，
•
=0，用S1、S2、S3分别表示△ABC、△ACD、ABD的面积，则S1+S2+S3的最大值是 ．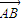
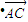=0，
•
=0，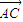
•
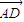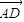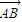=0，用S1、S2、S3分别表示△ABC、△ACD、ABD的面积，则S1+S2+S3的最大值是 ．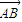
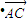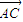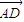=0，
•
=0，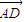
•
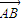=0，用S1、S2、S3分别表示△ABC、△ACD、ABD的面积，则S1+S2+S3的最大值是 ．