题目内容
(本题满分16分)已知ABCD四点的坐标分别为 A(1,0), B(4,3),
C(2,4),D(0,2)
⑴证明四边形ABCD是梯形;
⑵求COS∠DAB。
⑶设实数t满足( -t
-t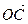 )·
)·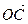 =0,求t的值。
=0,求t的值。
C(2,4),D(0,2)
⑴证明四边形ABCD是梯形;
⑵求COS∠DAB。
⑶设实数t满足(
 -t
-t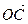 )·
)·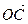 =0,求t的值。
=0,求t的值。⑴∵ =(3 3),
=(3 3),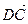 =(2 2) ……………………………………3′
=(2 2) ……………………………………3′
∴ =
=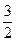
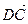
∴│ │=
│=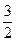 │
│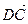 │且AB//CD
│且AB//CD
∴四边形ABCD是梯形 ……………………………………5′
⑵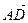 =(-1 2),
=(-1 2), =(3 3)
=(3 3)
∴COS∠DAB=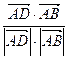 =
=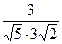 =
=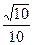 …………………………10′
…………………………10′
⑶ -t
-t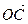 =(3 3)-t(2 4)=(3-2t 3-4t)………………12′
=(3 3)-t(2 4)=(3-2t 3-4t)………………12′
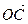 =(2 4)
=(2 4)
∴( -t
-t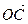 )·
)·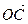 =0
=0 2(3-2t)+4(3-4t)=0
2(3-2t)+4(3-4t)=0
∴t=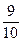 …………………………………………………………………16
…………………………………………………………………16
 =(3 3),
=(3 3),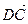 =(2 2) ……………………………………3′
=(2 2) ……………………………………3′∴
 =
=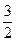
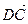
∴│
 │=
│=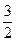 │
│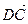 │且AB//CD
│且AB//CD∴四边形ABCD是梯形 ……………………………………5′
⑵
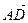 =(-1 2),
=(-1 2), =(3 3)
=(3 3)∴COS∠DAB=
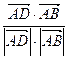 =
=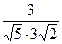 =
=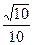 …………………………10′
…………………………10′⑶
 -t
-t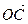 =(3 3)-t(2 4)=(3-2t 3-4t)………………12′
=(3 3)-t(2 4)=(3-2t 3-4t)………………12′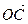 =(2 4)
=(2 4)∴(
 -t
-t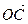 )·
)·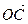 =0
=0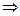 2(3-2t)+4(3-4t)=0
2(3-2t)+4(3-4t)=0∴t=
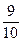 …………………………………………………………………16
…………………………………………………………………16略

练习册系列答案
相关题目
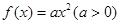 ,使得
,使得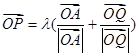 (
( 为常数),这里点P、Q的坐标分别为
为常数),这里点P、Q的坐标分别为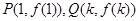 ,则k的取值范围为( )
,则k的取值范围为( )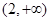
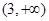


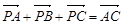 ,则( )
,则( )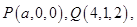 且
且 则
则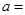 ( )
( )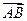 的坐标及|
的坐标及|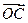 =
=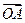 +
+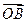 ,
,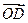 =
= ?
? .
. ,求
,求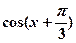 的值;
的值;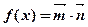 ,在
,在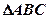 中,角
中,角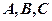 的对边分别为
的对边分别为 ,且满足
,且满足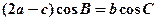 ,求
,求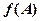 的取值范围.
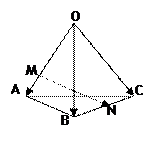
的取值范围.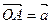 ,
,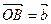 ,
,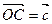 ,点M在OA上,且
,点M在OA上,且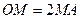 ,N是BC的中点,则
,N是BC的中点,则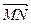 等于(
等于(  )
)
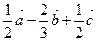
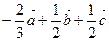
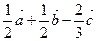
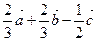
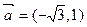 ,
,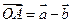 ,
, ,若△
,若△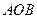 是以
是以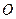 为直角顶点的等腰直角三角形,则△
为直角顶点的等腰直角三角形,则△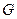 是
是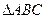 的重心,且
的重心,且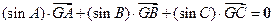 ,则
,则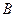 的大小为( )
的大小为( )