题目内容
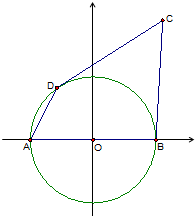
 如图,AB为平面直角坐标系xOy中单位圆O的直径,点D在第二象限内的圆弧上运动,CD与圆O相切,切点为D,且CD=AB.设∠DAB=θ,问当θ取何值时,四边形ABCD的面积最大?并求出这个最大值.
如图,AB为平面直角坐标系xOy中单位圆O的直径,点D在第二象限内的圆弧上运动,CD与圆O相切,切点为D,且CD=AB.设∠DAB=θ,问当θ取何值时,四边形ABCD的面积最大?并求出这个最大值.
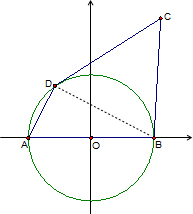 解:连接BD,
解:连接BD,∵AB为平面直角坐标系xOy中单位圆O的直径,点D在第二象限内的圆弧上运动
∴AD=2cosθ,BD=2sinθ(其中
 <θ<
<θ< ).…(2分)
).…(2分)在△BCD中,由弦切角定理得∠BDC=θ,又DC=AB=2,
∴△BCD面积为2sin2θ; …(4分)
又Rt△ABD的面积为2sinθ•cosθ.…(5分)
∴四边形ABCD的面积为S=2sinθ•cosθ+2sin2θ.…(6分)
因为S=sin2θ+(1-cos2θ) …(8分)
=
 sin(2θ-
sin(2θ- )+1 …(10分)
)+1 …(10分)∴
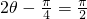 ,四边形ABCD面积取得最大值
,四边形ABCD面积取得最大值所以当θ=
 时,四边形ABCD面积取得最大值
时,四边形ABCD面积取得最大值 +1.…(12分)
+1.…(12分)分析:把四边形ABCD的面积分为两部分:△BCD面积与Rt△ABD的面积,分别计算它们的面积,再利用辅助角公式化简即可求得.
点评:本题以实际问题为载体,考查三角函数模型的构建,考查辅助角公式的运用,正确运用三角函数式解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y
已知长方形ABCD,AB=6,BC=7/4.以AB的中点0为原点建立如图所示的平面直角坐标系x0y 如图,AB为平面直角坐标系xOy中单位圆O的直径,点D在第二象限内的圆弧上运动,CD与圆O相切,切点为D,且CD=AB.设∠DAB=θ,问当θ取何值时,四边形ABCD的面积最大?并求出这个最大值.
如图,AB为平面直角坐标系xOy中单位圆O的直径,点D在第二象限内的圆弧上运动,CD与圆O相切,切点为D,且CD=AB.设∠DAB=θ,问当θ取何值时,四边形ABCD的面积最大?并求出这个最大值.