题目内容
对定义域是Df.Dg的函数y=f(x).y=g(x),规定:函数h(x)=
|
(1)若函数f(x)=
| 1 |
| x-1 |
(2)求问题(1)中函数h(x)的值域;
(3)若g(x)=f(x+α),其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos4x,并予以证明.
分析:(1)将f(x)=
,g(x)=)=x2,代入h(x)=
(2)利用双勾函数的性质求得;(3)令f(x)=sin2x+cos2x,α=
| 1 |
| x-1 |
|
| π |
| 4 |
解答:解:(1)h(x)=
,.
(2)当x≠1时,h(x)=
=x-1+
+2,
若x>1时,则h(x)≥4,其中等号当x=2时成立
若x<1时,则h(x)≤0,其中等号当x=0时成立
∴函数h(x)的值域是(-∞,0]∪{1}∪[4,+∞)
(3)令f(x)=sin2x+cos2x,α=
则g(x)=f(x+α)=sin2(x+
)+cos2(x+
)=cos2x-sin2x,
于是h(x)=f(x)•f(x+α)=(sin2x+cos2x)(cos2x-sin2x)=cos4x.
另解令f(x)=1+
sin2x,α=
,
g(x)=f(x+α)=1+
sin2(x+π)=1-
sin2x,
于是h(x)=f(x)•f(x+α)=(1+
sin2x)(1-
sin2x)=cos4x.
|
(2)当x≠1时,h(x)=
| x2 |
| x-1 |
| 1 |
| x-1 |
若x>1时,则h(x)≥4,其中等号当x=2时成立
若x<1时,则h(x)≤0,其中等号当x=0时成立
∴函数h(x)的值域是(-∞,0]∪{1}∪[4,+∞)
(3)令f(x)=sin2x+cos2x,α=
| π |
| 4 |
则g(x)=f(x+α)=sin2(x+
| π |
| 4 |
| π |
| 4 |
于是h(x)=f(x)•f(x+α)=(sin2x+cos2x)(cos2x-sin2x)=cos4x.
另解令f(x)=1+
| 2 |
| π |
| 2 |
g(x)=f(x+α)=1+
| 2 |
| 2 |
于是h(x)=f(x)•f(x+α)=(1+
| 2 |
| 2 |
点评:本题主要考查求函数解析式和求最值以及构造函数等问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式; .
. ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式; .
.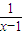 ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式; .
. ,g(x)=x2,写出函数h(x)的解析式;
,g(x)=x2,写出函数h(x)的解析式;