题目内容
在平面直角坐标系上,设不等式组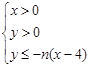 所表示的平面区域为
所表示的平面区域为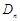 ,记
,记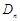 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为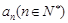 . 则
. 则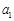 = ,经推理可得到
= ,经推理可得到 = .
= .
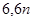
解析试题分析:根据题意,由x>0,y>0,-n(x-4)≥y>0得0<x≤4,
所以平面区域为Dn内的整点为点(4,0)与在直线x=1和x=2上,
∴直线y=-n(x-4)与直线x=1和x=2,x=3交点纵坐标分别为y1=3n和y2="2n," y3=n
∴Dn内在直线x=1和x=2上的整点个数分别为3n和2n,n
∴an=3n+2n+n=6n
当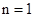 时,区域内的整点个数分别为6个,经推理可得到共
时,区域内的整点个数分别为6个,经推理可得到共 =
= ,故答案为6,6n。
,故答案为6,6n。
考点:本题主要考查了平面区域内整点个数的问题的运用。
点评:解决该试题的关键是理解不等式对于x的限定范围,然后分别对于x令值为1,2,3,得到整点的数,相加即为所求。

练习册系列答案
相关题目
 在过
在过 两点的直线
两点的直线 上,则实数
上,则实数 的值为 .
的值为 .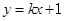 与以A(3,2)、B(2,3)为端点的线段有公共点,则k的取值范围是_________.
与以A(3,2)、B(2,3)为端点的线段有公共点,则k的取值范围是_________.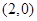 到直线
到直线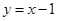 的距离为___ __。
的距离为___ __。 ,若直线
,若直线 过点
过点 ,且与线段
,且与线段 相交,则直线
相交,则直线 的直线的斜率是
的直线的斜率是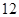 ,则
,则 的值为 。
的值为 。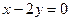 平行,则此直线的斜率为____________。
平行,则此直线的斜率为____________。