题目内容
经过直线2x+3y-7=0与7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程是___.
3x+6y-2=0
解析试题分析:联立方程组可知2x+3y-7=0与7x+15y+1=0的交点,为(12,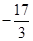 )
)
设所求直线为x+2y+m=0,则12+2×(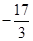 )+m=0,m=
)+m=0,m=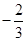 ,
,
故所求直线方程为:3x+6y-2=0
考点:本题主要是考查求两条直线的交点的方法,以及由平行直线系方程,利用待定系数法求直线的方程的方法.属于基础题.
点评:解决该试题的关键是先求出两直线的交点坐标,设出所求的直线方程x+2y+m=0,把交点坐标代入求出m,进而得到所求的直线方程.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 与直线
与直线 垂直,那么实数
垂直,那么实数 .
. 与直线
与直线 垂直,则实数a= 。
垂直,则实数a= 。 的倾斜角为 .
的倾斜角为 .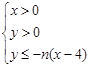 所表示的平面区域为
所表示的平面区域为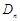 ,记
,记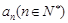 . 则
. 则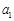 = ,经推理可得到
= ,经推理可得到 = .
= .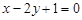 关于直线
关于直线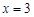 对称的直线方程为 .
对称的直线方程为 .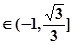 ,则直线l的倾斜角的范围是______________.
,则直线l的倾斜角的范围是______________.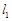 :
: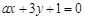 ,
,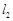 :
: 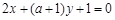 ,若
,若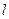 过点(—4,0)且与圆
过点(—4,0)且与圆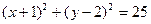 交于
交于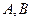 两点,如果
两点,如果 ,那么直线
,那么直线