题目内容
已知f(x)=lnx-ax2-bx(a≠0),(1)若a=-1,函数f(x)在其定义域内是增函数,求b的取值范围.
(2)在(1)的结论下,设g(x)=e2x+bex,x∈[0,ln2],求函数g(x)的最小值;
(3)设各项为正的数列{an}满足:a1=1,an+1=lnan+an+2,n∈N*,求证:an≤2n-1.
【答案】分析:(1)令导函数大于等于0恒成立,分离参数b,构造函数,利用基本不等式求出函数的最小值,令b小于等于最小值即可.
(2)令t=ex,将g(x)转化为二次函数,通过对二次函数的对称轴与区间的位置关系的讨论,求出g(x)的最小值.
(3)先求出输数列的前三项的值,归纳出大于等于0,利用数学归纳法证得成立,构造函数F(x),利用导数求出F(x)的最值,得到lnan≤an-1,得证.
解答:解:(1)依题意:f(x)=lnx+x2-bx
∵f(x)在(0,+∞)递增
∴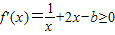 对x∈(0,+∞)恒成立
对x∈(0,+∞)恒成立
∴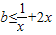
∵x>0
∴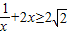 当且仅当
当且仅当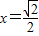 时取“=”,
时取“=”,
∴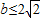 ,
,
且当 时,
时, ,
, ,
,
∴符合f(x)在(0,+∞)是增函数∴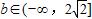
(2)设t=ex,
∵x∈[0,ln2]
∴1≤t≤2,
则函数g(x)化为: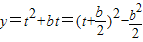 ,t∈[1,2]
,t∈[1,2]
①当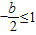 时,即
时,即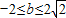 时.y在[1,2]递增∴当t=1时,ymin=b+1
时.y在[1,2]递增∴当t=1时,ymin=b+1
②当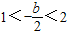 时,即-4<b<-2,当
时,即-4<b<-2,当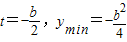
③当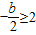 ,即b≤-4时,y在[1,2]递减,当t=2时,ymin=4+2b
,即b≤-4时,y在[1,2]递减,当t=2时,ymin=4+2b
综上: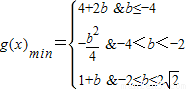
(3)∵a1=1,a2=ln1+1+2=3>1,a3=ln3+3+2>1
假设ak≥1(n≥1),则ak+1=lnak+ak+2>1,∴an≥1成立
设F(x)=lnx-x+1,(x≥1),则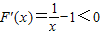
∴F(x)在[1,+∞]单调递减,∴F(x)≤F(1)=0,∴lnx≤x-1
∴lnan≤an-1,故an+1≤2an+1,∴an+1+1≤2(an+1)an+1+1≤2(an+1)≤22(an-1+1)≤≤2n(a1+1)=2n+1,
∴an+1≤2n⇒an≤2n-1
点评:解决函数在区间上单调常转化为导函数大于等于0或小于等于0恒成立;证明不等式常通过构造函数,利用导数求函数的最值证得.
(2)令t=ex,将g(x)转化为二次函数,通过对二次函数的对称轴与区间的位置关系的讨论,求出g(x)的最小值.
(3)先求出输数列的前三项的值,归纳出大于等于0,利用数学归纳法证得成立,构造函数F(x),利用导数求出F(x)的最值,得到lnan≤an-1,得证.
解答:解:(1)依题意:f(x)=lnx+x2-bx
∵f(x)在(0,+∞)递增
∴
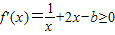 对x∈(0,+∞)恒成立
对x∈(0,+∞)恒成立∴
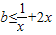
∵x>0
∴
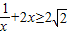 当且仅当
当且仅当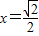 时取“=”,
时取“=”,∴
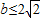 ,
,且当
 时,
时, ,
, ,
,
∴符合f(x)在(0,+∞)是增函数∴
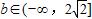
(2)设t=ex,
∵x∈[0,ln2]
∴1≤t≤2,
则函数g(x)化为:
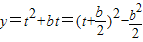 ,t∈[1,2]
,t∈[1,2]①当
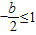 时,即
时,即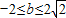 时.y在[1,2]递增∴当t=1时,ymin=b+1
时.y在[1,2]递增∴当t=1时,ymin=b+1②当
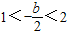 时,即-4<b<-2,当
时,即-4<b<-2,当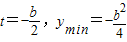
③当
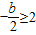 ,即b≤-4时,y在[1,2]递减,当t=2时,ymin=4+2b
,即b≤-4时,y在[1,2]递减,当t=2时,ymin=4+2b综上:
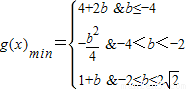
(3)∵a1=1,a2=ln1+1+2=3>1,a3=ln3+3+2>1
假设ak≥1(n≥1),则ak+1=lnak+ak+2>1,∴an≥1成立
设F(x)=lnx-x+1,(x≥1),则
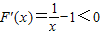
∴F(x)在[1,+∞]单调递减,∴F(x)≤F(1)=0,∴lnx≤x-1
∴lnan≤an-1,故an+1≤2an+1,∴an+1+1≤2(an+1)an+1+1≤2(an+1)≤22(an-1+1)≤≤2n(a1+1)=2n+1,
∴an+1≤2n⇒an≤2n-1
点评:解决函数在区间上单调常转化为导函数大于等于0或小于等于0恒成立;证明不等式常通过构造函数,利用导数求函数的最值证得.

练习册系列答案
相关题目