Question

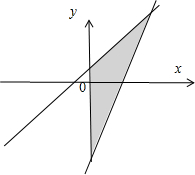
（文科做）曲线y=x²上的某点处的切线倾斜角为45°，经过改点的切线方程与y轴及直线2x-y-3=0所围成的三角形的面积是（　　）

• A．

  35

  4

• B．9
• C．

  35

  8

• D．4

Answer 1

分析：求出曲线的导数，利用曲线切线的斜率，求出切点坐标，推出切线方程，解出三角形的顶点坐标，然后求出三角形的面积．

解答：解：曲线y=x²，所以y′=2x，
设该切点坐标（x₀，y₀），则k=2x₀=tan45°=1，
解得：x0=

1

2

，
所以该点坐标为(

1

2

，

1

4

)，
切线方程为y=x+

1

2

，联立方程组

y=x+ 1 2 2x-y-3=0

，
解得

x= 5 2 y=2

，
三角形的一个顶点坐标为（

5

2

，2），
切线y=x+

1

2

与y轴的交点为（0，

1

2

），

直线2x-y-3=0与y轴的交点为（0，-3），
所以面积S=

1

2

×

7

2

×

5

2

=

35

8

．
故选C．

点评：本题是中档题，考查函数与导数的关系，三角形的面积的求法，考查计算能力．