题目内容
函数y=8sinxcosxcos2x的周期为T，最大值为A，则（ ）A．T=π，A=4
B．
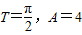
C．T=π，A=2
D．
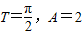
【答案】分析：利用二倍角公式吧函数的解析式化为2sin4x，再根据函数y=Asin（ωx+φ）的图象的周期性和最大值求得T和A的值．
解答：解：由于函数y=8sinxcosxcos2x=4sin2x•cos2x=2sin4x 的周期为T，∴T=
=
，且函数的最大值为 A=2，
故选D．
点评：本题主要考查二倍角公式的应用，函数y=Asin（ωx+φ）的图象的周期性和最大值，属于中档题．
解答：解：由于函数y=8sinxcosxcos2x=4sin2x•cos2x=2sin4x 的周期为T，∴T=
=，且函数的最大值为 A=2，故选D．
点评：本题主要考查二倍角公式的应用，函数y=Asin（ωx+φ）的图象的周期性和最大值，属于中档题．
练习册系列答案
相关题目
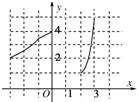13、函数y=f（x）的图象如图所示．那么，f（x）的定义域是