题目内容
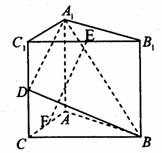
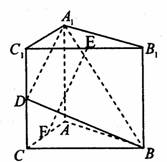
如下图,在直三棱柱ABC—A1B1C1中,底面是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.
(1)求A1B与平面ABD所成角的余弦值;
(2)求点A1到平面AED的距离.
解:(1)连结BG,则BG是BE在面ABD内的射影,即∠A1BG是A1B与平面ABD所成的角.

如图所示建立空间直角坐标系,坐标原点为C.设CA=2a,则A(2a,0,0),B(0,2a,0),D(0,0,1),A1(2a,0,2),E(a,a,1),G(![]() ).
).
∴![]()
∴![]() 解得a=1.
解得a=1.
∴![]() =(2,-2,2),
=(2,-2,2),![]() =(
=(![]() ).
).
∴cos∠A1BG=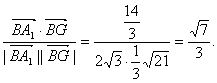
(2)由(1)有A(2,0,0),A1(2,0,2),E(1,1,1),D(0,0,1),
![]() =(-1,1,1)·(-1,-1,0)=0,
=(-1,1,1)·(-1,-1,0)=0,
![]() =(0,0,2)·(-1,-1,0)=0,
=(0,0,2)·(-1,-1,0)=0,
∴ED⊥平面AA1E.又ED![]() 平面AED,
平面AED,
∴平面AED⊥平面AA1E.
又面AED∩面AA1E=AE,
∴点A1在平面AED的射影K在AE上.
设![]() =(-λ,λ,λ-2).
=(-λ,λ,λ-2).
由![]() ,即λ+λ+λ-2=0,
,即λ+λ+λ-2=0,
解得λ=![]() .
.
∴![]()
![]()
∴![]()
![]()
故点A1到平面AED的距离为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是________.
,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是________.