题目内容
在曲线y=x2+1的图象上取一点（1，2）及附近一点（1+Δx，2+Δy），则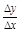
为 ．
【答案】
Δx+2
【解析】
试题分析：此题应用函数值的变化量与自变量的变化量的比值求得。根据题意，由于函数y=x2+1，那么可知：△y：△x=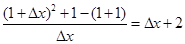
，故可知填写Δx+2
考点：变化率的概念
点评：通过计算函数值的变化来解，比较简单．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
在曲线y=x2+1的图象上取一点（1，2）及邻近一点（1+△x，2+△y），则△y：△x为（ ）
A、△x+
| ||
B、△x-
| ||
| C、△x+2 | ||
D、2+△x-
|
为( )
+2 B.Δx-
-2
为（ ）
+2
-2