题目内容
已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b一c)=0,则|c|的最大值是
| A.1 | B. | C.2 | D. |
D
解析试题分析:因为 ,又
,又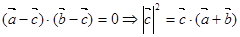
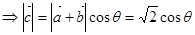
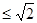 ,所以
,所以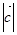 的最大值为
的最大值为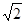
考点:平面向量的数量积的坐标表示、模、夹角
点评:本题的关键是充分利用已知条件和数量积的性质,借助向量模的性质得到要求向量模的最大值.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
平面向量 ,
, ,若
,若 与
与 共线,则
共线,则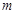 的值为( )
的值为( )
A.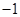 | B.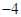 | C.1 | D.4 |
设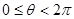 ,已知两个向量
,已知两个向量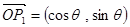 ,
,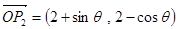 ,则向量
,则向量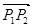 长度的最大值是( )
长度的最大值是( )
A.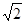 | B.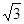 | C.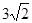 | D.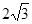 |
平面向量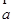 与
与 的夹角为
的夹角为 ,
, ,则
,则 =( )
=( )
A. | B.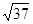 | C.7 | D.3 |
已知向量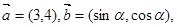 且
且 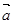 //
//  ,则
,则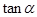 =( )
=( )
A.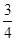 | B.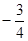 | C.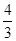 | D.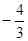 |
已知平面向量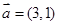 ,
,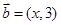 ,且
,且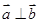 ,则实数
,则实数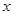 的值为
的值为
A.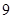 | B. | C.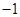 | D.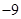 |
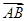 ·
·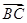 =3,△ABC的面积S∈[
=3,△ABC的面积S∈[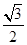 ,
, ],则
],则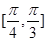
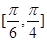
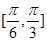
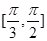
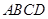 的顶点
的顶点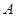 ,
,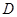 分别在
分别在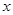 轴、
轴、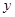 轴正半轴上移动,则
轴正半轴上移动,则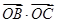 的最大值是( )
的最大值是( )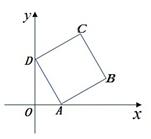
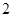
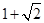
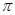
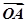 =
=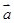 ,
,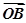 =
=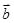 ,其中
,其中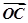 =λ
=λ