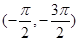题目内容
如右图,定圆半径为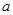 ,圆心为
,圆心为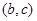 ,则直线
,则直线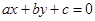 与直线
与直线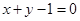 的交点在( )
的交点在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
D
解析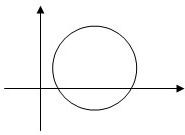
分析:先求出两直线的交点的坐标,由题中的图象可知,b>a>c,再判断交点的横坐标、纵坐标的符号,从而得到
两直线的交点所在的象限.
解:把直线ax+by+c=0与直线x+y-1="0" 联立方程组,解得它们的交点坐标为(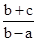 ,
,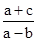 ),
),
由题中的图象可知,b>a>c,故有 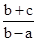 >0,
>0,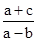 <0,
<0,
∴交点(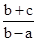 ,
,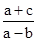 ) 在第四象限,
) 在第四象限,
故选 D.
点评:本题考查求两直线的交点的坐标的方法,通过考查交点的横坐标、纵坐标的符号,判断交点所在的象限.
关键是解读图象信息,得到b>a>c,体现了数形结合数学思想.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
在直角坐标系中,直线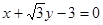 的倾斜角是( )
的倾斜角是( )
A.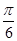 | B.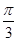 | C.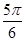 | D.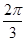 |
一条直线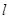 经过点
经过点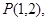 且与两点
且与两点 的距离相等,则直线
的距离相等,则直线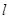 的方程是( )
的方程是( )
A.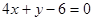 或 或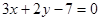 | B.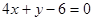 |
C.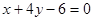 或 或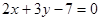 | D.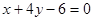 |
直线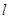 与直线
与直线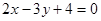 垂直,则直线
垂直,则直线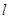 的方程可能是( )
的方程可能是( )
A. | B.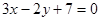 |
C.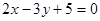 | D. |
点(2,1)到直线3x -4y + 2 = 0的距离是
A.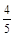 | B. | C.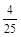 | D. |
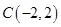 ,过点C作两条互相垂直的直线
,过点C作两条互相垂直的直线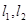 ,
,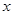 轴、
轴、 轴交于点A、
轴交于点A、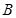 ,设点
,设点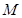 是线段
是线段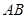 的中点,则点M的轨迹方程为( )
的中点,则点M的轨迹方程为( )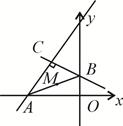
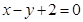 B.
B.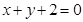
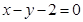 D.
D.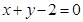
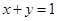 ,则
,则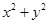 的最小值为 .
的最小值为 .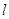 过
过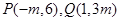 两点,且
两点,且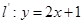 倾斜角的两倍,则实数
倾斜角的两倍,则实数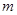 的值为( ▲ )
的值为( ▲ )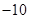
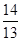
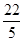
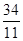
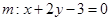 ,函数
,函数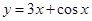 的图象与直线
的图象与直线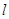 相切于P点,
相切于P点,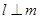 ,则P点的坐标可能是( )
,则P点的坐标可能是( )