题目内容
已知二项式(
+
(n∈N*)n(n∈N*)展开式中,前三项的二项式系数和是56,则展开式中的常数项为
.
| x | 2 |
| 1 | ||
2
|
| ) | n |
| 45 |
| 256 |
| 45 |
| 256 |
分析:由
+
+
=56,求得n,再利用二项展开式的通项公式即可求得展开式中的常数项.
| C | 0 n |
| C | 1 n |
| C | 2 n |
解答:解:由题意可得前三项的二项式系数和是
+
+
=56,即 1+n+
=56,
解得 n=10.
由于二项式(
+
(n∈N*)n(n∈N*)展开式的通项公式为 Tr+1=
•x20-2r•(
)r•x-
=(
)r•
•x20-
.
令20-
=0,求得 r=8,故展开式中的常数项为 (
)8•
=
,
故答案为
.
| C | 0 n |
| C | 1 n |
| C | 2 n |
| n(n-1) |
| 2 |
解得 n=10.
由于二项式(
| x | 2 |
| 1 | ||
2
|
| ) | n |
| C | r 10 |
| 1 |
| 2 |
| r |
| 2 |
| 1 |
| 2 |
| C | r 10 |
| 5r |
| 2 |
令20-
| 5r |
| 2 |
| 1 |
| 2 |
| C | 8 10 |
| 45 |
| 256 |
故答案为
| 45 |
| 256 |
点评:本题考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,求得n是关键,考查分析
运算能力,属于中档题.
运算能力,属于中档题.

练习册系列答案
相关题目
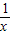 )n的展开式的二项式系数之和为32,则展开式中含x项的系数是 .
)n的展开式的二项式系数之和为32,则展开式中含x项的系数是 .