题目内容
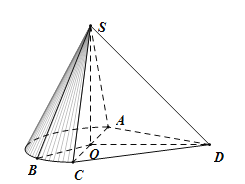
【题目】如图，已知四棱锥
，底面
为平行四边形，且
，点M为
的中点，
，且平面
平面.
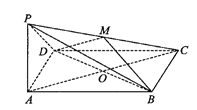
（1）求证：平面
平面
；
（2）当直线
与平面所成角的正切值为
时，求四棱锥的体积及平面
将四棱锥分成的两部分的体积比.
【答案】（1）证明见解析；（2）
.
【解析】
（1）根据给出的条件和余弦定理求出
的值，利用勾股定理可得
，即可证明
平面
，即可证明平面
平面；
（2）首先确定直线
与平面
所成角为
，再求出
，最后分别求出分成的两部分的体积，求出比值.
解：（1）证明：∵
，由余弦定理可得
，
∴
，
∴
.
∵平面
平面，
平面
平面
，
∴平面.
∵
平面
，
∴平面平面.
（2）过点P作
，点H为
中点，连接
，
∵平面平面，平面平面，
平面，则即为直线与平面所成角.
在
中，
，
∴
.
在
中，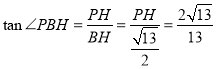
，
可得，
故
，
，
所以另一部分的体积
，
可知两部分的体积比为
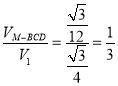或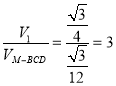
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某种水果按照果径大小可分为四类：标准果，优质果，精品果，礼品果.某采购商从采购的一批水果中随机抽取100个，利用水果的等级分类标准得到的数据如下：
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
（1）用样本估计总体，果园老板提出两种购销方案给采购商参考：
方案1：不分类卖出，单价为20元/
.
方案2：分类卖出，分类后的水果售价如下表：
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价（元/ | 16 | 18 | 22 | 24 |
从采购商的角度考虑，应该采用哪种方案较好？并说明理由.
（2）从这100个水果中用分层抽样的方法抽取10个，再从抽取的10个水果中随机抽取3个，
表示抽取到精品果的数量，求的分布列及数学期望
.
