题目内容
给定两个向量
与
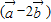平行，则x的值等于 ．
【答案】分析：由已知中向量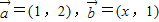
，我们可以求出向量
，
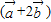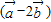的坐标，进而根据
∥
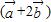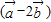，结合向量平行（共线）的充要条件，我们可以构造出一个关于x的方程，解方程求出x的值．
解答：解：∵向量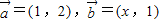
∴
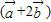=（2x+1，4）
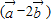=（1-2x，0）
又∵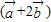
∥
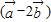
∴4•（1-2x）=0
解得x=
故答案为：
点评：本题考查的知识点是平面向量共线（平行）的坐标表示，其中根据已知求出两个平行向量的坐标，进而根据向量平行（共线）的充要条件，构造出关于x的方程，是解答本题的关键．
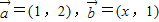，我们可以求出向量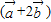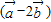，的坐标，进而根据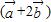∥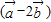，结合向量平行（共线）的充要条件，我们可以构造出一个关于x的方程，解方程求出x的值．解答：解：∵向量
∴
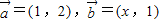
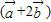=（2x+1，4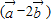）=（1-2x，0）又∵
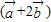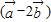
∥∴4•（1-2x）=0
解得x=
故答案为：
点评：本题考查的知识点是平面向量共线（平行）的坐标表示，其中根据已知求出两个平行向量的坐标，进而根据向量平行（共线）的充要条件，构造出关于x的方程，是解答本题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
给定两个向量
=(1，2)，
=(x，1)，若(
+2
)与(
-2
)平行，则x的值等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
，
，若
与
平行，则x的值等于
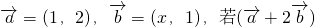与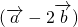
平行，则x的值等于________．