题目内容
过点M（1，2）的直线l将圆（x-2）2+y2=9分成两段弧，当其中的劣弧最短时，直线l的方程是
- A.x=1
- B.y=1
- C.x-y+1=0
- D.x-2y+3=0
D
分析：由条件知M点在圆内，故当劣弧最短时，l应与圆心与M点的连线垂直，求出直线的斜率即可．
解答：由条件知M点在圆内，故当劣弧最短时，l应与圆心与M点的连线垂直，
设圆心为O，则O（2，0），
∴KOM=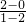
=-2．
∴直线l的斜率k=
，
∴l的方程为y-2=（x-1）．即x-2y+3=0；
故选D
点评：本题主要考查了直线的一般式方程，以及直线和圆的方程的应用，属于基础题．
分析：由条件知M点在圆内，故当劣弧最短时，l应与圆心与M点的连线垂直，求出直线的斜率即可．
解答：由条件知M点在圆内，故当劣弧最短时，l应与圆心与M点的连线垂直，
设圆心为O，则O（2，0），
∴KOM=
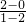=-2．∴直线l的斜率k=
，∴l的方程为y-2=
（x-1）．即x-2y+3=0；故选D
点评：本题主要考查了直线的一般式方程，以及直线和圆的方程的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
椭圆E：
过点A（a,0）,B(0,b)的直
，原点到该直线的距离为
.
求直线MN的方程；
交椭圆于P、Q两点，以PQ为直径的圆过点D（1，0）？若存在，求出k的值；若不存在，请说明理由。
=
，求△BDK的内切圆M的方程。
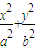=1（a＞b＞0）离心率为
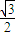，且过P（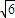
，
）．
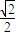，0），且与开口朝上，顶点在原点的抛物线C切于第二象限的一点N，直 线l与椭圆E交于A，B两点，与y轴交与D点，若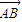
=
，
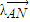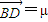
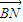，且λ+μ=
，求抛物线C的标准方程．