题目内容
已知椭圆C1:
+
=1(a>b>0)的右顶点为P(1,0),过C1的焦点且垂直长轴的弦长为1.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设抛物线C2:y=x2+h(h∈R)的焦点为F,过F点的直线l交抛物线与A、B两点,过A、B两点分别作抛物线C2的切线交于Q点,且Q点在椭圆C1上,求△ABQ面积的最值,并求出取得最值时的抛物线C2的方程.
| y2 |
| a2 |
| x2 |
| b2 |
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设抛物线C2:y=x2+h(h∈R)的焦点为F,过F点的直线l交抛物线与A、B两点,过A、B两点分别作抛物线C2的切线交于Q点,且Q点在椭圆C1上,求△ABQ面积的最值,并求出取得最值时的抛物线C2的方程.
分析:(Ⅰ)由已知得到b的值,结合通径长为1求得a的值,则椭圆方程可求;
(Ⅱ)设出A,B的坐标及切线AQ的方程y-(x12+h)=k(x-x1),和抛物线方程联立后由判别式等于0得到切线斜率与A的横坐标的关系,进一步得到AQ的方程,同理得到BQ的方程,联立两切线方程求出Q点的坐标,写出三角形ABQ的面积表达式,结合Q点在椭圆上把面积用含有k的代数式表示,求出使面积取得最值时的k与h值,则△ABQ面积取得最值时的抛物线C2的方程可求.
(Ⅱ)设出A,B的坐标及切线AQ的方程y-(x12+h)=k(x-x1),和抛物线方程联立后由判别式等于0得到切线斜率与A的横坐标的关系,进一步得到AQ的方程,同理得到BQ的方程,联立两切线方程求出Q点的坐标,写出三角形ABQ的面积表达式,结合Q点在椭圆上把面积用含有k的代数式表示,求出使面积取得最值时的k与h值,则△ABQ面积取得最值时的抛物线C2的方程可求.
解答:解:(I)由题意得
,解得
,
∴所求的椭圆方程为
+x2=1;
(II)令A(x1,x12+h),B(x2,x22+h),
设切线AQ方程为y-(x12+h)=k(x-x1),代入y=x2+h,得:x2-kx+kx1-x12=0.
令△=0,可得k=2x1.
∴抛物线C2在点A处的切线斜率为k=2x1.
∴切线AQ方程为:y-(x12+h)=2x1(x-x1),即y=2x1x-x12+h ①
同理可得BQ方程为:y=2x2x-x22+h ②
联立①②解得Q点为(
,x1x2+h).
焦点F坐标为(0,h+
),令l方程为:y=kx+h+
,代入C2:y=x2+h,
得:x2-kx-
=0,由韦达定理有:x1+x2=k,x1x2=-
.
∴Q点为(
,h-
).
过Q作y轴平行线交AB于M点,则S△ABQ=
|QM||x1-x2|.
M点为(
,
+h+
),
|QM|=
,|x1-x2|=
=
.
∴S△ABQ=
|QM||x1-x2|=
(
)3.
而Q点在椭圆上,∴
+(
)2=1,∴k2=4-(h-
)2∈[0,4].
∴(S△ABQ)min=
,此时k=0,h=
或-
,
则抛物线方程为:y=x2+
或y=x2-
.
(S△ABQ)max=
,此时k2=4,h=
,
则抛物线方程为:y=x2+
.
|
|
∴所求的椭圆方程为
| y2 |
| 4 |
(II)令A(x1,x12+h),B(x2,x22+h),
设切线AQ方程为y-(x12+h)=k(x-x1),代入y=x2+h,得:x2-kx+kx1-x12=0.
令△=0,可得k=2x1.
∴抛物线C2在点A处的切线斜率为k=2x1.
∴切线AQ方程为:y-(x12+h)=2x1(x-x1),即y=2x1x-x12+h ①
同理可得BQ方程为:y=2x2x-x22+h ②
联立①②解得Q点为(
| x1+x2 |
| 2 |
焦点F坐标为(0,h+
| 1 |
| 4 |
| 1 |
| 4 |
得:x2-kx-
| 1 |
| 4 |
| 1 |
| 4 |
∴Q点为(
| k |
| 2 |
| 1 |
| 4 |
过Q作y轴平行线交AB于M点,则S△ABQ=
| 1 |
| 2 |
M点为(
| k |
| 2 |
| k2 |
| 2 |
| 1 |
| 4 |
|QM|=
| k2+1 |
| 2 |
| (x1+x2)2-4x1x2 |
| k2+1 |
∴S△ABQ=
| 1 |
| 2 |
| 1 |
| 4 |
| k2+1 |
而Q点在椭圆上,∴
(h-
| ||
| 4 |
| k |
| 2 |
| 1 |
| 4 |
∴(S△ABQ)min=
| 1 |
| 4 |
| 9 |
| 4 |
| 7 |
| 4 |
则抛物线方程为:y=x2+
| 9 |
| 4 |
| 7 |
| 4 |
(S△ABQ)max=
5
| ||
| 4 |
| 1 |
| 4 |
则抛物线方程为:y=x2+
| 1 |
| 4 |
点评:本题考查了椭圆的标准方程的求法,考查了直线与圆锥曲线的位置关系,训练了设而不求的解题思想方法和数学转化思想方法,解答的关键是如何把三角形ABQ的面积转化为仅含直线AQ的斜率k的函数关系,考查了学生灵活处理问题的能力和整体计算能力,是高考试卷中的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
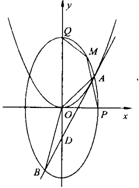 已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.
已知点D(0,-2),过点D作抛线C1:x2=2py(p>0)的切线l,切点A在第一象限,如图.