题目内容
 A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是
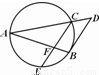
A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是B.(几何证明选讲选做题)如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=2
| 7 |
C.(坐标系与参数方程选做题)在极坐标系(ρ,θ)(0≤θ<2π)中,曲线
ρ=2sinθ与ρcosθ=-1的交点的极坐标为
分析:A、由题意知,k 只要大于|x+1|-|x-2|的最小值 即可,问题化为求|x+1|-|x-2|的最小值.
B、由圆的切线长定理 求得 BD 的长、及AD的长,△DBC 中,由余弦定理求出cos∠CDB 的值,△ACD中,由余弦定理求得 AC的长.
C、ρ=2sinθ与ρcosθ=-1的交点 即 x2+y2=2y 与 x=-1 的交点(-1,1),再把交点的坐标化为极坐标.
B、由圆的切线长定理 求得 BD 的长、及AD的长,△DBC 中,由余弦定理求出cos∠CDB 的值,△ACD中,由余弦定理求得 AC的长.
C、ρ=2sinθ与ρcosθ=-1的交点 即 x2+y2=2y 与 x=-1 的交点(-1,1),再把交点的坐标化为极坐标.
解答:解:A、因为存在实数x使不等式|x+1|-|x-2|<k成立,而|x+1|-|x-2|表示数轴上的x到-1的距离减去
它到2的距离,故|x+1|-|x-2|的最大值是3,最小值为-3,∴k>-3.
B、由圆的切线长定理得 (2
)2=BD•(BD+3),∴BD=4,∴AD=7,
△DBC 中,由余弦定理得 32=42+(2
)2-2×4×2
×cos∠CDB,
∴cos∠CDB=
,
△ACD中,由余弦定理得 AC2=(2
)2+72-2×2
×7cos∠CDB=
,
∴AC的长为
.
C、ρ=2sinθ与ρcosθ=-1的交点 即 x2+y2=2y 与 x=-1 的交点(-1,1),
此点的极坐标为(
,
).
故答案为 k>-3、
、(
,
).
它到2的距离,故|x+1|-|x-2|的最大值是3,最小值为-3,∴k>-3.
B、由圆的切线长定理得 (2
| 7 |
△DBC 中,由余弦定理得 32=42+(2
| 7 |
| 7 |
∴cos∠CDB=
5
| ||
| 16 |
△ACD中,由余弦定理得 AC2=(2
| 7 |
| 7 |
| 63 |
| 4 |
∴AC的长为
3
| ||
| 2 |
C、ρ=2sinθ与ρcosθ=-1的交点 即 x2+y2=2y 与 x=-1 的交点(-1,1),
此点的极坐标为(
| 2 |
| 3π |
| 4 |
故答案为 k>-3、
3
| ||
| 2 |
| 2 |
| 3π |
| 4 |
点评:本题考查绝对值的意义,圆的线长定理,余弦定理得应用,普通方程与极坐标方程的互化,体现了转化的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则线段CD的长为 .
,则线段CD的长为 .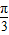 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .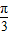 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .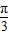 )的直角坐标是 .
)的直角坐标是 .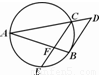
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .