题目内容
如图所示,已知圆E:x2+(y﹣1)2=4交x轴分别于A,B两点,交y轴的负半轴于点M,过点M作圆E的弦MN.
(1)若弦MN所在直线的斜率为2,求弦MN的长;
(2)若弦MN的中点恰好落在x轴上,求弦MN所在直线的方程;
(3)设弦MN上一点P(不含端点)满足PA,PO,PB成等比数列(其中O为坐标原点),试探求 的取值范围.
的取值范围.

解:(1)在圆E的方程中令x=0,得M(0,﹣1),
又KMN=2,
所以弦MN所在直线的方程为y+1=2x,即2x﹣y﹣1=0.
∵圆心到直线MN的距离为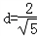 ,且r=2,
,且r=2,
∴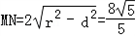 .
.
(2)因为yM+yN=0,所以yN=1,代入圆E的方程中得N(±2,1).
由M(0,﹣1),N(±2,1)得
直线MN的方程为x﹣y﹣1=0或x+y+1=0.
(3)易得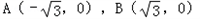 ,
,
设P(x,y),则由PA PB=PO2,得
PB=PO2,得
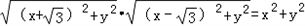 ,
,
化简得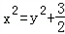 ①
①
由题意知点P在圆E内,所以x2+(y﹣1)2<4,
结合①,4y2﹣4y﹣3<0,
解得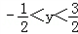 .
.
从而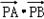 =
=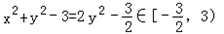 .
.
又KMN=2,
所以弦MN所在直线的方程为y+1=2x,即2x﹣y﹣1=0.
∵圆心到直线MN的距离为
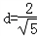 ,且r=2,
,且r=2,∴
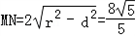 .
.(2)因为yM+yN=0,所以yN=1,代入圆E的方程中得N(±2,1).
由M(0,﹣1),N(±2,1)得
直线MN的方程为x﹣y﹣1=0或x+y+1=0.
(3)易得
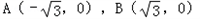 ,
,设P(x,y),则由PA
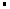 PB=PO2,得
PB=PO2,得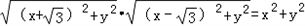 ,
,化简得
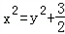 ①
①由题意知点P在圆E内,所以x2+(y﹣1)2<4,
结合①,4y2﹣4y﹣3<0,
解得
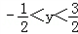 .
.从而
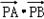 =
=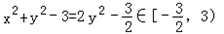 .
.
练习册系列答案
相关题目
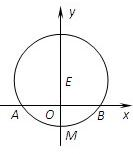 如图所示,已知圆E:x2+(y-1)2=4交x轴分别于A,B两点,交y轴的负半轴于点M,过点M作圆E的弦MN.
如图所示,已知圆E:x2+(y-1)2=4交x轴分别于A,B两点,交y轴的负半轴于点M,过点M作圆E的弦MN. 的取值范围.
的取值范围.
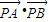 的取值范围.
的取值范围.
 的取值范围.
的取值范围.