题目内容
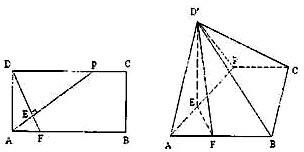
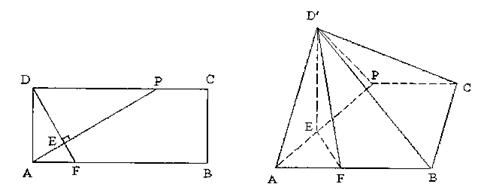
已知P在矩形ABCD边DC上,AB=2,BC=1,F在AB上且DF⊥AP,垂足为E,将△ADP沿AP折起.使点D位于D′位置,连D′B、D′C得四棱锥D′-ABCP.(I)求证D′F⊥AP;
(II)若PD=1并且平面D′AP⊥平面ABCP,求四棱锥D′-ABCP的体积.

【答案】分析:(1)此题属于“折叠”问题,解决这类问题的关键就在于紧紧把握住在两个折叠面内的垂直关系,因为这种关系是不变的.比如图中的AP⊥D'E,AP⊥EF,所以其实不管平面D'EF折叠到什么位置,AP⊥平面D'EF总是成立的,故AP⊥D'F也总是成立的
(2)解决棱锥求体积的问题,关键在于找到合适的高与对应的底面,切忌不审图形,盲目求解;由题目条件:平面D′AP⊥平面ABCP易得所求棱锥的高即为D'E,所以底面就是梯形ABCP,再运用棱锥体积公式就可以了
解答:证明:(I)∵AP⊥D'E,AP⊥EF,又∵D'E,EF是面D'EF内两相交直线∴AP⊥平面D'EF,∴AP⊥D'F(7分)
(II)∵PD=1,∴四边形ADPF是边长为1的正方形,
∴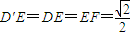 ,
,
∵平面D'AP⊥平面ABCP,D'E⊥AP,
∴D'E⊥平面ABCP,(11分)
∵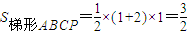 ,
,
∴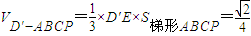 (14分)
(14分)
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.
(2)解决棱锥求体积的问题,关键在于找到合适的高与对应的底面,切忌不审图形,盲目求解;由题目条件:平面D′AP⊥平面ABCP易得所求棱锥的高即为D'E,所以底面就是梯形ABCP,再运用棱锥体积公式就可以了
解答:证明:(I)∵AP⊥D'E,AP⊥EF,又∵D'E,EF是面D'EF内两相交直线∴AP⊥平面D'EF,∴AP⊥D'F(7分)
(II)∵PD=1,∴四边形ADPF是边长为1的正方形,
∴
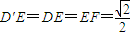 ,
,∵平面D'AP⊥平面ABCP,D'E⊥AP,
∴D'E⊥平面ABCP,(11分)
∵
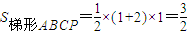 ,
,∴
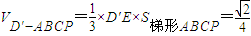 (14分)
(14分)点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(本小题满分12分)
已知P在矩形ABCD边DC上,AB=2,BC=1,F在AB上且DF ⊥AP,垂足为E,将△ADP沿AP折起.使点D位于D′位置,连D′B、D′C得四棱锥D′—ABCP.
(I)求证D′F⊥AP;
|