题目内容
函数 是[1,+∞)上的增函数.
是[1,+∞)上的增函数.(Ⅰ)求正实数a的取值范围;
(Ⅱ)若函数g(x)=x2+2x,在使g(x)≥M对定义域内的任意x值恒成立的所有常数M中,我们把M的最大值M=-1叫做f(x)=x2+2x的下确界,若函数
 的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.
的定义域为[1,+∞),根据所给函数g(x)的下确界的定义,求出当a=1时函数f(x)的下确界.(Ⅲ)设b>0,a>1,求证:

【答案】分析:①当函数单调递增时,其导数大于等于0恒成立求参数的范围
②求下确界就是求函数的最小值利用导数求函数的最值
③证明不等式就是求最值
解答:解:(1)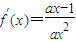
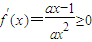 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,
∴ 对x∈[1,+∞)恒成立
对x∈[1,+∞)恒成立
又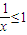 ∴a≥1答:
∴a≥1答:
正实数a的取值范围为a≥1
(2)由(1)可知a=1时,函数f(x)是定义域[1,+∞)上的增函数,
故f(x)min=f(1)=0,
f(x)≥M恒成立
∴M≤f(x)min=0
∴M的最大值为0,
∴当a=1时函数f(x)的下确界为0.
答:当a=1时函数f(x)的下确界是0
(3)取 ,∵
,∵ ,
,
由(1)知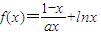 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,
∴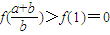
∴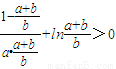 ,
,
即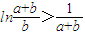
点评:导数的应用①知函数的单调性求参数范围 一般转化成道函数恒大于等于0 或小于等于0
②证明不等式转化成函数的最值,若含着对数或指数一般用导数求最值.
②求下确界就是求函数的最小值利用导数求函数的最值
③证明不等式就是求最值
解答:解:(1)
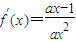
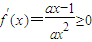 对x∈[1,+∞)恒成立,
对x∈[1,+∞)恒成立,∴
 对x∈[1,+∞)恒成立
对x∈[1,+∞)恒成立又
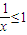 ∴a≥1答:
∴a≥1答:正实数a的取值范围为a≥1
(2)由(1)可知a=1时,函数f(x)是定义域[1,+∞)上的增函数,
故f(x)min=f(1)=0,
f(x)≥M恒成立
∴M≤f(x)min=0
∴M的最大值为0,
∴当a=1时函数f(x)的下确界为0.
答:当a=1时函数f(x)的下确界是0
(3)取
 ,∵
,∵ ,
,由(1)知
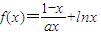 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,∴
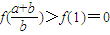
∴
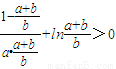 ,
,即
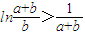
点评:导数的应用①知函数的单调性求参数范围 一般转化成道函数恒大于等于0 或小于等于0
②证明不等式转化成函数的最值,若含着对数或指数一般用导数求最值.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
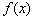
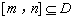

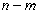
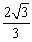
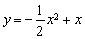
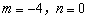
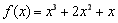
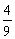
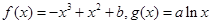 .
.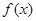 在
在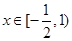 上的最大值为
上的最大值为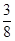 ,求实数
,求实数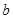 的值;
的值;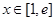 ,都有
,都有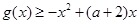 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;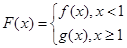 ,对任意给定的正实数
,对任意给定的正实数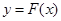 上是否存在两点
上是否存在两点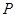 、
、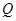 ,使得
,使得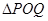 是以
是以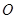 (
(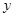 轴上?请说明理由。
轴上?请说明理由。 .
. 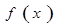 在
在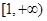 上是减函数;
上是减函数;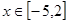 时,求
时,求