题目内容
(5分)(2011•福建)若a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx+2在x=1处有极值,则ab的最大值等于( )
| A.2 | B.3 | C.6 | D.9 |
D
解析试题分析:求出导函数,利用函数在极值点处的导数值为0得到a,b满足的条件;利用基本不等式求出ab的最值;注意利用基本不等式求最值需注意:一正、二定、三相等.
解:∵f′(x)=12x2﹣2ax﹣2b
又因为在x=1处有极值
∴a+b=6
∵a>0,b>0
∴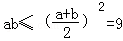
当且仅当a=b=3时取等号
所以ab的最大值等于9
故选D
点评:本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值需注意:一正、二定、三相等.

练习册系列答案
相关题目
函数y=x2cosx的导数为( )
| A.y′=2xcosx-x2sinx | B.y′=2xcosx+x2sinx |
| C.y′=x2cosx-2xsinx | D.y′=xcosx-x2sinx |
下列求导数运算正确的是( )
A.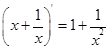 | B.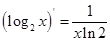 |
C.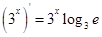 | D.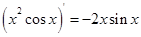 |
已知函数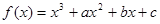 有两个极值点
有两个极值点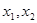 ,若
,若 ,则关于
,则关于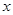 的方程
的方程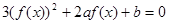 的不同实根个数为 ( )
的不同实根个数为 ( )
| A.3 | B.4 | C.5 | D.6 |
设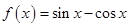 ,则
,则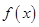 在
在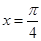 处的导数
处的导数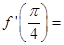 ( )
( )
A.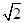 | B.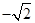 | C.0 | D. |
已知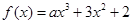 ,若
,若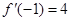 ,则
,则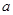 的值等于 ( )
的值等于 ( )
A.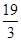 | B.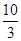 | C.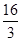 | D.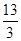 |
已知函数f(x)=1+x-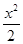 +
+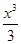 -
-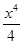 +…+
+…+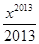 ,则下列结论正确的是( )
,则下列结论正确的是( )
| A.f(x)在(0,1)上恰有一个零点 |
| B.f(x)在(0,1)上恰有两个零点 |
| C.f(x)在(-1,0)上恰有一个零点 |
| D.f(x)在(-1,0)上恰有两个零点 |
 在区间(0,1)内任取两个实数p,q,且p≠q,不等式
在区间(0,1)内任取两个实数p,q,且p≠q,不等式 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )