题目内容
(本题满分14分)
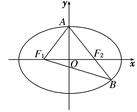
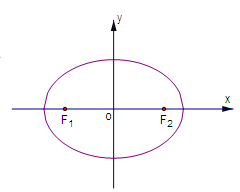
如图,已知椭圆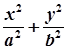 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若 =2
=2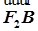 ,
,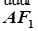 ·
·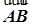 =
=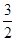 ,求椭圆的方程.
,求椭圆的方程.
如图,已知椭圆
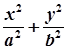 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若
 =2
=2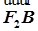 ,
,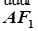 ·
·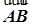 =
=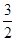 ,求椭圆的方程.
,求椭圆的方程.(1)e=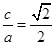 .(2)
.(2)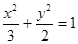
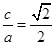 .(2)
.(2)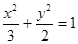
试题分析:解:(1)若∠F1AB=90°,则△AOF2为等腰直角三角形,所以有OA=OF2,
即b=c.所以a=
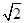 c,e=
c,e=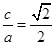 .
. (2)由题知A(0,b),F1(-c,0),F2(c,0),
其中,c=
 ,设B(x,y).
,设B(x,y).由
 =2
=2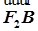 ?(c,-b)=2(x-c,y),解得x=
?(c,-b)=2(x-c,y),解得x=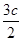 ,
,y=
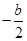 ,即B(
,即B(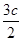 ,
,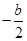 ).
). 将B点坐标代入
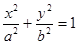 ,得
,得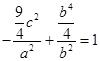 ,
,即
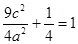 ,
,解得a2=3c2.①
又由
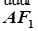 ·
·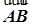 =(-c,-b)·(
=(-c,-b)·(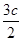 ,
,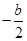 )=
)=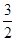
⇒b2-c2=1,
即有a2-2c2=1.②
由①,②解得c2=1,a2=3,从而有b2=2.
所以椭圆方程为
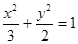 .
.点评:解决的关键是根据椭圆的定义以及三角形的性质得到a,b,c的关系式,同时结合向量的数量积来秋季诶得到其方程,属于基础题。

练习册系列答案
相关题目
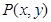 到直线
到直线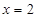 的距离与它到定点
的距离与它到定点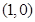 的距离之比为
的距离之比为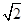 ,并记点
,并记点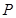 的轨迹为曲线
的轨迹为曲线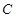 .
.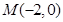 ,过点
,过点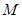 的直线
的直线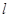 与曲线
与曲线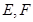 两点,当线段
两点,当线段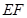 的中点落在由四点
的中点落在由四点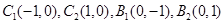 构成的四边形内(包括边界)时,求直线
构成的四边形内(包括边界)时,求直线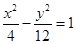 上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点距离是8,那么点P到它的左焦点的距离是( ) 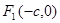 、
、 分别是椭圆
分别是椭圆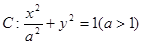 的左、右焦点,
的左、右焦点,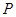 为椭圆
为椭圆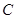 上任意一点,且
上任意一点,且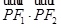 最小值为
最小值为 .
.
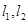 均与椭圆
均与椭圆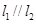 ,试探究在
,试探究在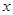 轴上是否存在定点
轴上是否存在定点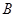 ,点
,点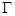 的方程为
的方程为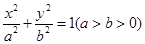 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).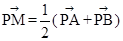 ,求点
,求点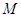 的坐标;
的坐标;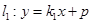 交椭圆
交椭圆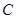 、
、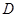 两点,交直线
两点,交直线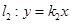 于点
于点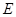 .若
.若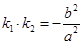 ,证明:
,证明: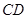 的中点;
的中点;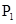 、
、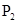 满足
满足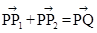 ,写出求作点
,写出求作点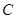 的中心为坐标原点
的中心为坐标原点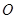 ,一个长轴端点为
,一个长轴端点为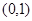 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线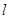 与
与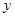 轴交于点
轴交于点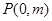 ,与椭圆
,与椭圆 ,且
,且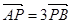 。(14分)
。(14分)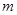 的取值范围。
的取值范围。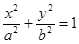 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F (1,0),离心率为
(1,0),离心率为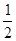 ,P为左顶点。
,P为左顶点。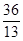 ,求直线AB的方程。
,求直线AB的方程。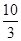 )与抛物线
)与抛物线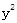 =2x上的点P的距离为
=2x上的点P的距离为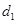 ,P到抛物线准线l的距为
,P到抛物线准线l的距为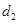 ,则
,则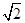 )
)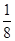 ,-
,-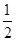 )
)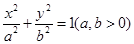 的焦点坐标为
的焦点坐标为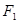 (
(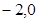 ),点M(
),点M(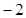 ,
,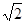 )在椭圆E上.
)在椭圆E上.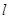 与椭圆E交于
与椭圆E交于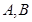 两点,求线段
两点,求线段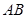 中点
中点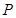 的轨迹方程;
的轨迹方程;