题目内容
如图，在正三棱柱ABCDEF中，AB＝2，AD＝1.P是CF的延长线上一点，FP＝t.过A、B、P三点的平面交FD于M，交FE于N.
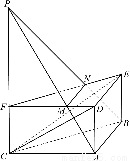
(1)求证：MN∥平面CDE；
(2)当平面PAB⊥平面CDE时，求t的值．
（1）见解析（2）t＝2
【解析】(1)证明：因为AB∥DE，AB在平面FDE外，所以AB∥平面FDE.又MN是平面PAB与平面FDE的交线，所以AB∥MN，故MN∥DE.因为MN?平面CDE，DE
平面CDE，所以MN∥平面CDE.
(2)【解析】
取AB中点G、DE中点H，连结GH，则由GH∥PC知P、C、G、H在同一平面上，并且由PA＝PB知PG⊥AB.而与(1)同理可证AB平行于平面PAB与平面CDE的交线，因此，PG也垂直于该交线．又平面PAB⊥平面CDE，所以PG⊥平面CDE，所以PG⊥CH，于是△CGH∽△PCG，所以
，即
，解得t＝2.
练习册系列答案
相关题目
