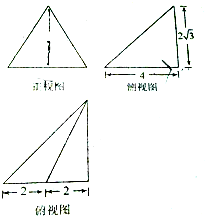
题目内容
14.已知函数f(x)=x(ex-e-x)-(2x-1)(e2x-1-e1-2x),则满足f(x)>0的实数x的取值范围为($\frac{1}{3}$,1).分析 根据条件构造函数g(x),利用函数的奇偶性和单调性的性质解不等式即可
解答 解:构造函数g(x)=x(ex-e-x),
则g(x)=x(ex-e-x)为偶函数,且当x>0时,g(x)单调递增,
则由f(x)>0,得x(ex-e-x)>(2x-1)(e2x-1-e1-2x),
即g(x)>g(2x-1),
∴不等式等价为g(|x|)>g(|2x-1|),
即|x|>|2x-1|,
即x2>(2x-1)2,
∴3x2-4x+1<0,
解得:$\frac{1}{3}$<x<1,
故答案为:($\frac{1}{3}$,1).
点评 本题主要考查不等式的解法,利用条件构造函数,利用函数的奇偶性和单调性是解决本题的关键

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
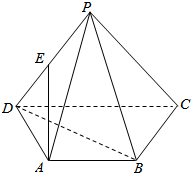 如图,在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥CD,∠ADC=$\frac{π}{3}$,PD=PC=CD=2AB=2,E为PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥CD,∠ADC=$\frac{π}{3}$,PD=PC=CD=2AB=2,E为PD的中点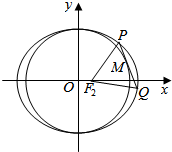 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F2(1,0),点H(2,$\frac{{2\sqrt{10}}}{3}$)在椭圆上.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F2(1,0),点H(2,$\frac{{2\sqrt{10}}}{3}$)在椭圆上. 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的一个顶点恰好在抛物线x2=8y的准线上.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的一个顶点恰好在抛物线x2=8y的准线上.