题目内容
(12分)某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ;第二组
;第二组![]() ……第五组
……第五组![]() .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设![]() 、
、![]() 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知![]() .
.
求事件“![]() ”的概率.
”的概率.
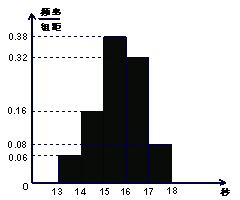
解析:(Ⅰ)由直方图知,成绩在![]() 内的人数为:
内的人数为:![]() (人)
(人)
所以该班成绩良好的人数为27人.…………4分
(Ⅱ)由直方图知,成绩在![]() 的人数为
的人数为![]() 人,设为
人,设为![]() 、
、![]() 、
、![]() ;
;
成绩在![]() 的人数为
的人数为![]() 人,设为
人,设为![]() 、
、![]() 、
、![]() 、
、![]() .……………6分
.……………6分
若![]() 时,有
时,有![]() 3种情况;
3种情况;
若![]() 时,有
时,有![]() 6种情况;
6种情况;
若![]() 分别在
分别在![]() 和
和![]() 内时,
内时,
| A | B | C | D |
x | xA | xB | xC | xD |
y | yA | yB | yC | yD |
z | zA | zB | zC | zD |
共有12种情况. …………………………10分
所以基本事件总数为21种,事件“![]() ”所包含的基本事件个数有12种.
”所包含的基本事件个数有12种.
∴P(![]() )=
)=![]() …………………………12分
…………………………12分

练习册系列答案
相关题目
(本小题满分12分)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按以下方法分成五组:第一组![]() ,第二组
,第二组![]() ,----,第五组
,----,第五组![]() ,且已知频率分布表如右
,且已知频率分布表如右
| 分组 | 频数 | 频率 |
|
| 3 | |
|
|
| |
|
| 0.38 | |
|
|
| |
|
|
| |
| 合计 | 50 | 1 |
(1)求![]() 的值;
的值;
(2)若成绩大于或等于14秒且小于16秒认为
良好,求百米测试中成绩良好的人数;
(3)若从第一、五组中随机取出两人成绩,求这两人成绩差的绝对值大于3秒的概率。
 50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
50名学生在一模数学考试中,成绩都属于区间[60,110]。将成绩按如下方式分成五组:第一组[60,70);第二组[70,80);第三组[80,90);第四组[90,100);第五组[100,110]。部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
 ,求
,求 的概率;
的概率; ;第二组
;第二组 ……第五组
……第五组 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图. 
 、
、 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知 .
. ”的概率.
”的概率. ;第二组
;第二组 ……第五组
……第五组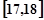 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图. 
 、
、 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知 .
. ”的概率.
”的概率. ,第二组
,第二组 ,…,第五组
,…,第五组 .下图是按上述分组方法得到的频率分布直方图。
.下图是按上述分组方法得到的频率分布直方图。
 内的所有学生中随机抽取两名同学,设其测试成绩分别为
内的所有学生中随机抽取两名同学,设其测试成绩分别为 ,
, ,求事件“
,求事件“ ”概率.
”概率.