题目内容
在 中,点
中,点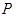 在
在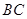 上,且
上,且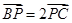 ,点
,点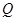 是
是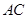 的中点,若
的中点,若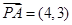 ,
,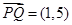 ,则
,则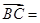 ( )
( )
A.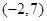 | B.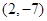 | C.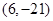 | D.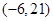 |
D
解析试题分析:设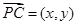 .因为
.因为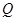 是
是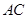 的中点,所以
的中点,所以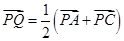 ,即
,即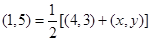 ,解得
,解得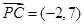 ,
,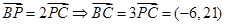 .
.
考点:1.平面向量的基本定理;2.向量运算的坐标表示.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
与向量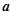 =(1,-3,2)平行的一个向量的坐标为( )
=(1,-3,2)平行的一个向量的坐标为( )
| A.(1,3,2) | B.(-1,-3,2) | C.(-1,3,-2) | D.(1,-3,-2) |
已知平面向量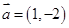 ,
,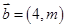 ,且
,且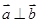 ,则向量
,则向量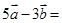 ( )
( )
A.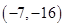 | B.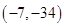 | C.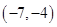 | D.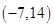 |
已知平面向量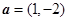 ,
,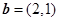 ,
,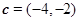 ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.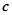 ∥ ∥ |
B.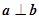 |
C.对同一平面内的任意向量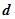 ,都存在一对实数 ,都存在一对实数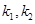 ,使得 ,使得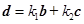 |
D.向量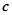 与向量 与向量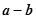 的夹角为 的夹角为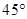 |
设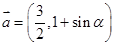 ,
,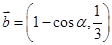 ,且
,且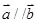 ,则锐角
,则锐角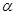 为( )
为( )
A.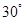 | B.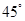 | C. | D.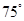 |
平行四边形 中,
中, =(1,0),
=(1,0), =(2,2),则
=(2,2),则 等于( )
等于( )
| A.4 | B.-4 | C.2 | D.-2 |
如图所示,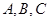 是圆
是圆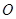 上的三点,线段
上的三点,线段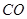 的延长线于线段
的延长线于线段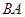 的延长线交于圆
的延长线交于圆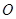 外的一点
外的一点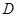 ,若
,若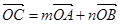 ,则
,则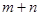 的取值范围是( )
的取值范围是( )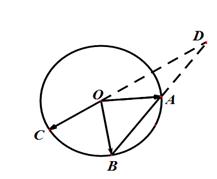
A.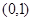 | B.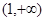 | C. | D.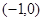 |
设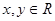 ,向量
,向量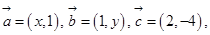 且
且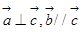 ,则
,则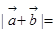 ( )
( )
A.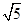 | B.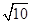 | C.2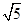 | D.10 |
 ,其中
,其中 与
与 的夹角为
的夹角为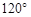 ,
, 的夹角为
的夹角为 ,且
,且 ,若
,若 ,则( )
,则( )



