题目内容
已知圆C方程为:x2+y2=4.(Ⅰ)直线l过点P(1,2),且与圆C交于A、B两点,若
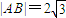 ,求直线l的方程;
,求直线l的方程;(Ⅱ)过圆C上一动点M作平行于x轴的直线m,设m与y轴的交点为N,若向量
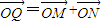 ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
【答案】分析:(I)分类讨论:①当直线l垂直于x轴时;②若直线l不垂直于x轴.对于②,设其方程为y-2=k(x-1),结合直线与圆的位置关系利用弦长公式即可求得k值,从而解决问题.
(II)设点M的坐标为(x,y)(y≠0),Q点坐标为(x,y),利用向量的坐标运算表示出M的坐标,再利用M点在圆上其坐标适合方程即可求得动点Q的轨迹方程,最后利用方程的形式进行判断是什么曲线即可.
解答:解(Ⅰ)①当直线l垂直于x轴时,
则此时直线方程为x=1,l与圆的两个交点坐标为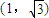 和
和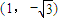 ,
,
其距离为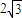 满足题意(1分)
满足题意(1分)
②若直线l不垂直于x轴,设其方程为y-2=k(x-1),即kx-y-k+2=0
设圆心到此直线的距离为d,则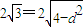 ,得d=1(3分)
,得d=1(3分)
∴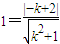 ,
,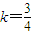 ,
,
故所求直线方程为3x-4y+5=0
综上所述,所求直线为3x-4y+5=0或x=1(7分)
(Ⅱ)设点M的坐标为(x,y)(y≠0),Q点坐标为(x,y)
则N点坐标是(0,y)(9分)
∵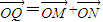 ,
,
∴(x,y)=(x,2y)即x=x,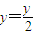 (11分)
(11分)
又∵x2+y2=4,∴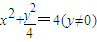
∴Q点的轨迹方程是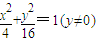 ,(13分)
,(13分)
轨迹是一个焦点在x轴上的椭圆,除去短轴端点.(14分)
点评:本小题主要考查直线的一般式方程、直线和圆的方程的应用、轨迹方程的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.
(II)设点M的坐标为(x,y)(y≠0),Q点坐标为(x,y),利用向量的坐标运算表示出M的坐标,再利用M点在圆上其坐标适合方程即可求得动点Q的轨迹方程,最后利用方程的形式进行判断是什么曲线即可.
解答:解(Ⅰ)①当直线l垂直于x轴时,
则此时直线方程为x=1,l与圆的两个交点坐标为
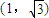 和
和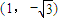 ,
,其距离为
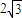 满足题意(1分)
满足题意(1分)②若直线l不垂直于x轴,设其方程为y-2=k(x-1),即kx-y-k+2=0
设圆心到此直线的距离为d,则
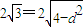 ,得d=1(3分)
,得d=1(3分)∴
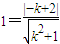 ,
,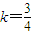 ,
,故所求直线方程为3x-4y+5=0
综上所述,所求直线为3x-4y+5=0或x=1(7分)
(Ⅱ)设点M的坐标为(x,y)(y≠0),Q点坐标为(x,y)
则N点坐标是(0,y)(9分)
∵
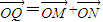 ,
,∴(x,y)=(x,2y)即x=x,
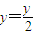 (11分)
(11分)又∵x2+y2=4,∴
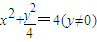
∴Q点的轨迹方程是
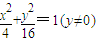 ,(13分)
,(13分)轨迹是一个焦点在x轴上的椭圆,除去短轴端点.(14分)
点评:本小题主要考查直线的一般式方程、直线和圆的方程的应用、轨迹方程的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
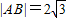 ,求直线l的方程;
,求直线l的方程;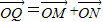 ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线. ,求直线l的方程;
,求直线l的方程; ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.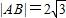 ,求直线l的方程;
,求直线l的方程; ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.