题目内容
如果对于函数![]() 的定义域内任意的
的定义域内任意的![]() ,都有
,都有![]() 成立,那么就称函数
成立,那么就称函数![]() 是定义域上的“平缓函数”.(1)判断函数
是定义域上的“平缓函数”.(1)判断函数![]() ,
,![]() 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数![]() 是闭区间
是闭区间![]() 上的“平缓函数”,且
上的“平缓函数”,且![]() .证明:对于任意的
.证明:对于任意的![]()
![]() ,都有
,都有![]() 成立.(3)设
成立.(3)设![]() 、
、![]() 为实常数,
为实常数,![]() .若
.若![]() 是区间
是区间![]() 上的“平缓函数”,试估计
上的“平缓函数”,试估计![]() 的取值范围(用
的取值范围(用![]() 表示,不必证明).
表示,不必证明).
(Ⅰ) 是 (Ⅱ) 见解析 (Ⅲ)![]()
解析:
:(1)对于任意的![]()
![]() ,有
,有![]() ,
,![]() .………2分
.………2分
从而![]() .
.
∴函数![]() ,
,![]() 是“平缓函数”. ………………………4分
是“平缓函数”. ………………………4分
(2)当![]() 时,由已知得
时,由已知得![]() ; ………6分
; ………6分
当![]() 时,因为
时,因为![]()
![]() ,不妨设
,不妨设![]() ,其中
,其中![]() ,因为
,因为![]() ,所以
,所以![]()
![]()
![]()
![]()
![]()
![]() .
.
故对于任意的![]()
![]() ,都有
,都有![]() 成立. ……………1
成立. ……………1![]() 0分
0分
(3)结合函数![]() 的图象性质及其在点
的图象性质及其在点![]() 处的切线斜率,估计
处的切线斜率,估计![]() 的取值范围是闭区间
的取值范围是闭区间![]() ………(注:只需直接给出正确结论)………14分
………(注:只需直接给出正确结论)………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
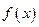 的定义域内的任意
的定义域内的任意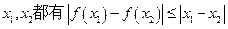 成立,那么就称函数
成立,那么就称函数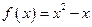 ,
,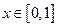 是否是 “平缓函数”?
是否是 “平缓函数”?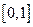 上的“平缓函数”,且
上的“平缓函数”,且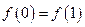 .证明:对任意的
.证明:对任意的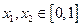 都有
都有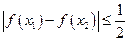 .
.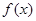 的定义域内任意一个
的定义域内任意一个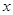 的值,均有
的值,均有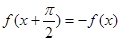 ,且
,且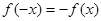 ,对于下列五个函数:①
,对于下列五个函数:①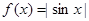 ;②
;②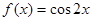 ; ③
; ③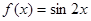 ;④
;④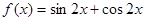 ,其中适合题设条件的函数的序号是 .
,其中适合题设条件的函数的序号是 .