题目内容
若关于x，y的方程组
有实数解，则k的取值范围是
|
[-
，
]
| 5 |
| 2 |
| 5 |
| 2 |
[-
，
]
．| 5 |
| 2 |
| 5 |
| 2 |
分析：由
⇒x2-5x+k2=0?△≥0，从而可求得k的取值范围．
|
解答：解：∵
有解，
∴等价于x2-5x+k2=0有解?△=25-4k2≥0，
解得：-
≤k≤
．
故答案为：[-
，
]．
|
∴等价于x2-5x+k2=0有解?△=25-4k2≥0，
解得：-
| 5 |
| 2 |
| 5 |
| 2 |
故答案为：[-
| 5 |
| 2 |
| 5 |
| 2 |
点评：本题考查基本不等式，关键是对“x2-5x+k2=0有实数解”的理解与应用，属于基础题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
若关于x，y的方程组
有实数解，则实数a，b满足（ ）
|
| A、a2+b2＞1 |
| B、a2+b2≥1 |
| C、a2+b2≤1 |
| D、a2+b2＜1 |
有解，且所有的解都是整数，则有序数对（a，b）所对应的点的个数为（ ）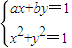
有实数解，则实数a，b满足（ ）