题目内容
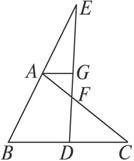
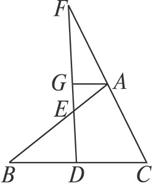
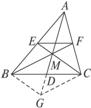
如图1-2-18(1)，已知AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明
+
=
成立(不要求证明),若将图1-2-18(1)中的垂直改为斜交，如图1-2-18(2)，AB∥CD，AD、BC相交于点E，过E作EF∥AB，交BD于点F，则(1)
+
=
还成立吗？如果成立，请给出证明；如果不成立，请说明理由.
(2)请找出S△ABD、S△BED和S△BDC间的关系式，并给出证明.
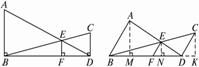
图1-2-18
思路解析:本题一是通过阅读发现题中蕴含着类比猜想的思想方法，因而易猜想关系式仍成立；二是有一处伏笔“不要求证明”，具有一定的迷惑性，因为论证猜想是否成立，还需“同样的方法”.
证明:（1）成立.∵AB∥EF,?
∴=.?
∵CD∥EF,∴=.?
∴+ =
+
=
=1.?
∴
+
=
.?
（2）关系式为
+
=
.?
分别过A作AM⊥BD于M，过E作EN⊥BD于N，过C作CK⊥BD交BD的延长线于K.
由题设可得
+
=
,
+
=
.?
∵
BD·AM =S△ABD,
BD·CK =S△BCD,
BD·EN =S△BED?,?
∴
+
=
.
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
+
=
成立(不要求证明),若将图1-2-18(1)中的垂直改为斜交，如图1-2-18(2)，AB∥CD，AD、BC相交于点E，过E作EF∥AB，交BD于点F，则?
ED=FD
EG;
