题目内容
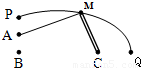
如图,A村在B地正北 km处,C村在B地正东4km处,已知弧形公路PQ上任一点到B,C距离之和为8km,现要在公路旁建造一个供电所M分别向A村、C村送电,但C村有一村办工厂用电需用专用线路,不得与民用混线用电,因此向C村要架两条线路分别给村民和工厂送电.
km处,C村在B地正东4km处,已知弧形公路PQ上任一点到B,C距离之和为8km,现要在公路旁建造一个供电所M分别向A村、C村送电,但C村有一村办工厂用电需用专用线路,不得与民用混线用电,因此向C村要架两条线路分别给村民和工厂送电.(1)试指出公路PQ所在曲线的类型,并说明理由;
(2)要使得所用电线最短,供电所M应建在A村的什么方位,并求出M到A村的距离.
【答案】分析:(1)根据题意得|MB|+|MC|=8(8>|BC|=4),结合椭圆的定义得出M在以B,C为焦点,长轴长为8的椭圆上;
(2)建立如图所示的坐标系,则B(-2,0),C(2,0),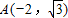 ,从而得出椭圆方程为
,从而得出椭圆方程为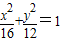 ,作MN⊥l于N,则
,作MN⊥l于N,则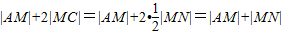 ,由平面几何知识知,当直线MN通过A时,|AM|+|MN|最小从而解决问题.
,由平面几何知识知,当直线MN通过A时,|AM|+|MN|最小从而解决问题.
解答: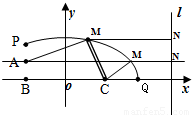 解:(1)∵|MB|+|MC|=8(8>|BC|=4),
解:(1)∵|MB|+|MC|=8(8>|BC|=4),
∴M在以B,C为焦点,长轴长为8的椭圆上;
(2)建立如图所示的坐标系,
则B(-2,0),C(2,0),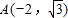 ,
,
求得椭圆方程为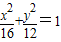 ,
,
其离心率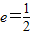 ,右准线为l:x=8.
,右准线为l:x=8.
作MN⊥l于N,则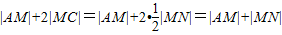 ,
,
由平面几何知识知,当直线MN通过A时,|AM|+|MN|最小为|AN|,此时M的纵坐标为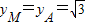 ,
,
∴M的横坐标为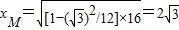 .
.
故得M在A正东且距A为(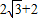 )km处.
)km处.
点评:考查圆锥曲线的实际背景及作用、考查学生根据实际问题选择函数类型的能力,以及会用椭圆的定义的方法来求函数的最小值的能力.
(2)建立如图所示的坐标系,则B(-2,0),C(2,0),
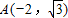 ,从而得出椭圆方程为
,从而得出椭圆方程为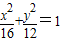 ,作MN⊥l于N,则
,作MN⊥l于N,则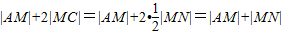 ,由平面几何知识知,当直线MN通过A时,|AM|+|MN|最小从而解决问题.
,由平面几何知识知,当直线MN通过A时,|AM|+|MN|最小从而解决问题.解答:
 解:(1)∵|MB|+|MC|=8(8>|BC|=4),
解:(1)∵|MB|+|MC|=8(8>|BC|=4),∴M在以B,C为焦点,长轴长为8的椭圆上;
(2)建立如图所示的坐标系,
则B(-2,0),C(2,0),
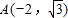 ,
,求得椭圆方程为
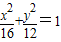 ,
,其离心率
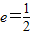 ,右准线为l:x=8.
,右准线为l:x=8.作MN⊥l于N,则
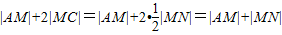 ,
,由平面几何知识知,当直线MN通过A时,|AM|+|MN|最小为|AN|,此时M的纵坐标为
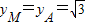 ,
,∴M的横坐标为
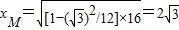 .
.故得M在A正东且距A为(
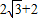 )km处.
)km处.点评:考查圆锥曲线的实际背景及作用、考查学生根据实际问题选择函数类型的能力,以及会用椭圆的定义的方法来求函数的最小值的能力.

练习册系列答案
相关题目
 如图,A村在B地正北
如图,A村在B地正北
 如图,A村在B地正北
如图,A村在B地正北