题目内容
对于在区间A上有意义的两个函数f(x)和g(x),如果对任意的x∈A,恒有|f(x)-g(x)|≤1,则称f(x)与g(x)在A上是接近的,否则称f(x)与g(x)在A上是非接近的.
(1)证明:函数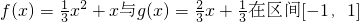 上是接近的;
上是接近的;
(2)若函数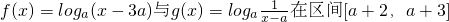 上是接近的,求实数a的取值范围.
上是接近的,求实数a的取值范围.
解:(1)证明:当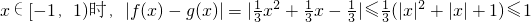
故f(x)与g(x)在[-1,1]上是接近的
(2)f(x)与g(x)在[a+2,a+3]上是接近的?对任意的x∈[a+2,a+3],恒有
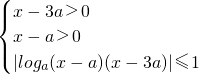 …①…②…③
…①…②…③
由①②恒成立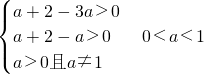
③恒成立?-1≤logn(x-a)(x-3a)≤1(x∈[a+2,a+3])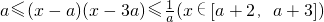
由0<a<1知2a<a+2,故函数?(x)=(x-a)(x-3a)
在[a+2,a+3]上递增,因此有
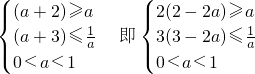
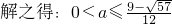
综上所述得a的取值范围是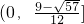 .
.
分析:(1)欲证明证明:函数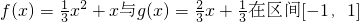 上是接近的;只须证明:当
上是接近的;只须证明:当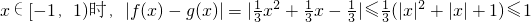 即可;
即可;
(2)由于f(x)与g(x)在[a+2,a+3]上是接近的?对任意的x∈[a+2,a+3],恒有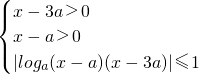 下面分别讨论此三个不等式恒成立的条件即可得到a的取值范围.
下面分别讨论此三个不等式恒成立的条件即可得到a的取值范围.
点评:本小题主要考查对数函数的性质和应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想,解题时要注意函数恒成立的充要条件的合理运用.
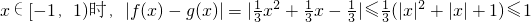
故f(x)与g(x)在[-1,1]上是接近的
(2)f(x)与g(x)在[a+2,a+3]上是接近的?对任意的x∈[a+2,a+3],恒有
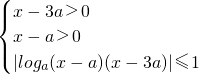 …①…②…③
…①…②…③由①②恒成立
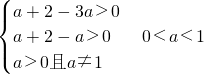
③恒成立?-1≤logn(x-a)(x-3a)≤1(x∈[a+2,a+3])
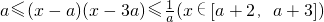
由0<a<1知2a<a+2,故函数?(x)=(x-a)(x-3a)
在[a+2,a+3]上递增,因此有

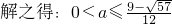
综上所述得a的取值范围是
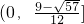 .
.分析:(1)欲证明证明:函数
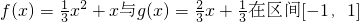 上是接近的;只须证明:当
上是接近的;只须证明:当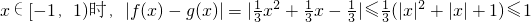 即可;
即可;(2)由于f(x)与g(x)在[a+2,a+3]上是接近的?对任意的x∈[a+2,a+3],恒有
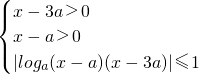 下面分别讨论此三个不等式恒成立的条件即可得到a的取值范围.
下面分别讨论此三个不等式恒成立的条件即可得到a的取值范围.点评:本小题主要考查对数函数的性质和应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想,解题时要注意函数恒成立的充要条件的合理运用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
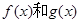 ,如果对任意的
,如果对任意的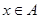 ,恒有
,恒有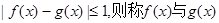 在A上是接近的,否则称
在A上是接近的,否则称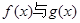 在A上是非接近的。
在A上是非接近的。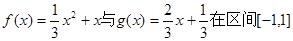 上是接近的;
上是接近的;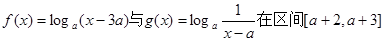 上是接近的,求实数a的取值范围。
上是接近的,求实数a的取值范围。