题目内容
设f(x)在x0处可导,下列式子中与f′(x0)相等的是( )
(1)
;(2)
;
(3)
(4)
.
(1)
| lim |
| △x→0 |
| f(x0)-f(x0-2△x) |
| 2△x |
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| △x |
(3)
| lim |
| △x→0 |
| f(x0+2△x)-f(x0+△x) |
| △x |
| lim |
| △x→0 |
| f(x0+△x)-f(x0-2△x) |
| △x |
| A、(1)(2) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(2)(3)(4) |
分析:根据导数的定义一个一个地进行验证可知(1)和(3)的值都是f′(x0);(2)的值是2f′(x0).(4)的值是3f′(x0).
由此可知正确答案是B.
由此可知正确答案是B.
解答:解:(1)
=
=f′(x0).
(2)
=
=2f′(x0).
(3)
=f′(x0).
(4)
=
=3f′(x0).
故选B.
| lim |
| △x→0 |
| f(x0)-f(x0-2△x) |
| 2△x |
| lim |
| 2△x→0 |
| f(x0+2△x-2△x)-f(x0-2△x) |
| 2△x |
(2)
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| △x |
| lim |
| △x→0 |
| f(x0-△x+2△x)-f(x0-△x) |
| △x |
(3)
| lim |
| △x→0 |
| f(x0+2△x)-f(x0+△x) |
| △x |
(4)
| lim |
| △x→0 |
| f(x0+△x)-f(x0-2△x) |
| △x |
| lim |
| △x→0 |
| f(x0-2△x+3△x)-f(x0-2△x) |
| △x |
故选B.
点评:本题考查导数的定义,解题时要熟练地理解导数的定义.

练习册系列答案
相关题目
设函数f(x)在x0处可导,则
等于( )
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| △x |
| A、f′(x0) |
| B、f′(-x0) |
| C、-f′(x0) |
| D、-f(-x0) |
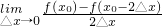 ;(2)
;(2)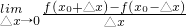 ;
;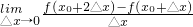 (4)
(4)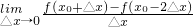 .
. ;
; ;
; ;
; 。
。