题目内容
(1)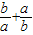 ≥2成立当且仅当a,b均为正数.
≥2成立当且仅当a,b均为正数.(2)
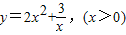 的最小值是
的最小值是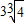 .
.(3)
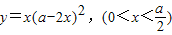 的最大值是
的最大值是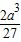 .
.(4)|a+
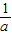 |≥2成立当且仅当a≠0.
|≥2成立当且仅当a≠0.以上命题是真命题的是: .
【答案】分析:由于当a,b均为负数时,不等式仍成立,故(1)不正确;
(2)不正确,因为利用基本不等式求得函数的最小值等于3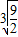 .
.
(3)正确,由基本不等式可求得函数的最大值是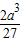 .
.
(4)正确 )|a+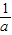 |≥2成立当且仅当|a|+
|≥2成立当且仅当|a|+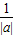 ≥2,当且仅当 a≠0.
≥2,当且仅当 a≠0.
解答:解:(1)不正确,因为当a,b均为负数时,不等式仍成立.
(2)不正确,因为 当x>0时,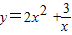 =
=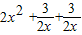 ≥3
≥3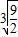 ,故函数的最小值等于3
,故函数的最小值等于3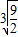 .
.
(3)正确,∵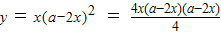 ≤
≤
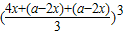 =
= •
•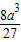 =
=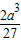 ,
,
(4)|a+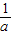 |≥2成立当且仅当|a|+
|≥2成立当且仅当|a|+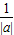 ≥2,当且仅当 a≠0,故(4)正确.
≥2,当且仅当 a≠0,故(4)正确.
故答案为 (3)(4).
点评:本题考查基本不等式在最值中的应用,要注意使用条件以及检验等号能否成立.
(2)不正确,因为利用基本不等式求得函数的最小值等于3
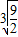 .
.(3)正确,由基本不等式可求得函数的最大值是
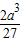 .
.(4)正确 )|a+
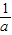 |≥2成立当且仅当|a|+
|≥2成立当且仅当|a|+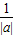 ≥2,当且仅当 a≠0.
≥2,当且仅当 a≠0.解答:解:(1)不正确,因为当a,b均为负数时,不等式仍成立.
(2)不正确,因为 当x>0时,
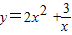 =
=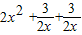 ≥3
≥3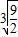 ,故函数的最小值等于3
,故函数的最小值等于3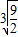 .
.(3)正确,∵
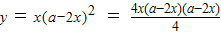 ≤
≤
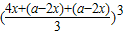 =
= •
•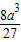 =
=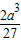 ,
,(4)|a+
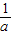 |≥2成立当且仅当|a|+
|≥2成立当且仅当|a|+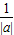 ≥2,当且仅当 a≠0,故(4)正确.
≥2,当且仅当 a≠0,故(4)正确.故答案为 (3)(4).
点评:本题考查基本不等式在最值中的应用,要注意使用条件以及检验等号能否成立.

练习册系列答案
相关题目
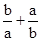 ≥2成立当且仅当a,b均为正数.(2)
≥2成立当且仅当a,b均为正数.(2)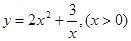 的最小值是
的最小值是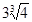 (3)
(3)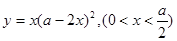 的最大值是
的最大值是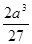 (4)|a+
(4)|a+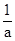 |≥2成立当且仅当a≠0.
|≥2成立当且仅当a≠0.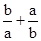 ≥2成立当且仅当a,b均为正数.(2)
≥2成立当且仅当a,b均为正数.(2)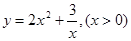 的最小值是
的最小值是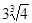 .
.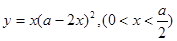 的最大值是
的最大值是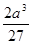 .(4)|a+
.(4)|a+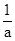 |≥2成立当且仅当a≠0.
|≥2成立当且仅当a≠0.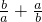 ≥2成立当且仅当a,b均为正数.
≥2成立当且仅当a,b均为正数.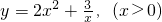 的最小值是
的最小值是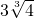 .
.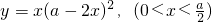 的最大值是
的最大值是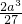 .
. |≥2成立当且仅当a≠0.
|≥2成立当且仅当a≠0.