题目内容
在任意八边形ABCDEFGT中,取各边中点,如图,H、I、J、K、L、M、N、O分别是GT、TA、AB、BC、CD、DE、EF、FG的中点,连接IK、JL、MO、NH,P、Q、R、S分别是NH、MO、JL、IK的中点.求证:以P、Q、R、S为顶点的四边形SRQP是平行四边形.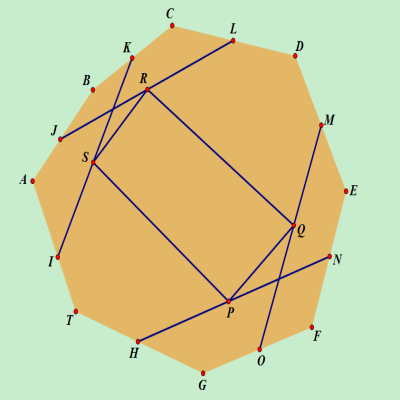
分析:取AD的中点X,连接JX、JK、KL、LX,由三角形的中位线定理可得:四边形JKLX是平行四边形.对角线JL与KX相交于点R.由三角形的中位线定理可得:SR∥TD.同理可知:PQ∥TD.得到SR∥PQ.同理可证:SP∥RQ.即可证明.
解答:证明:如图所示,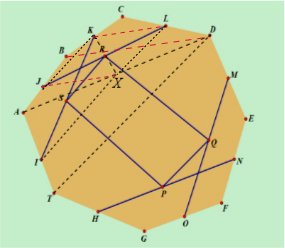
取AD的中点X,连接JX、JK、KL、LX,
由三角形的中位线定理可得:JX
BD
KL,
∴JX
KL,
∴四边形JKLX是平行四边形.
∴对角线JL与KX相交于点R.
由三角形的中位线定理可得:SR∥IX,IX∥TD,
∴SR∥TD.
同理可知:PQ∥TD.
∴SR∥PQ.
同理可证:SP∥RQ.
∴以P、Q、R、S为顶点的四边形SRQP是平行四边形.

取AD的中点X,连接JX、JK、KL、LX,
由三角形的中位线定理可得:JX
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴JX
| ∥ |
. |
∴四边形JKLX是平行四边形.
∴对角线JL与KX相交于点R.
由三角形的中位线定理可得:SR∥IX,IX∥TD,
∴SR∥TD.
同理可知:PQ∥TD.
∴SR∥PQ.
同理可证:SP∥RQ.
∴以P、Q、R、S为顶点的四边形SRQP是平行四边形.
点评:本题考查了三角形的中位线定理、平行四边形定理的判定与性质定理,考查了添加辅助线的能力,考查了推理能力,考查了处理复杂问题的能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
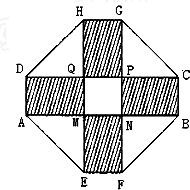 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.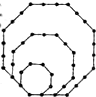 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是 某小区要建一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的十字形地域,四个小矩形加一个正方形面积共为200平方米.计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺设花岗岩地坪,造价为每平方米210元,再在四个角上铺设草坪,造价为每平方米80元.
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的十字形地域,四个小矩形加一个正方形面积共为200平方米.计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺设花岗岩地坪,造价为每平方米210元,再在四个角上铺设草坪,造价为每平方米80元. (2006•上海模拟)某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域,计划在正方形MNPQ上建一座观景花坛,造价为4200元/平方米,在四个相同的矩形上铺花岗岩地评,造价为210元/平方米,再在四个空角上铺草坪,造价为80元/平方米.
(2006•上海模拟)某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域,计划在正方形MNPQ上建一座观景花坛,造价为4200元/平方米,在四个相同的矩形上铺花岗岩地评,造价为210元/平方米,再在四个空角上铺草坪,造价为80元/平方米.