题目内容
已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(Ⅰ)证明:BN⊥平面C1B1N;
(Ⅱ)设直线C1N与平面CNB1所成的角为![]() ,求sin
,求sin![]() 的值;
的值;
(Ⅲ)M为AB中点,在CB上是否存在一点P,使得MP∥平面CNB1,若存在,求出BP的长;若不存在,请说明理由.

(Ⅱ) ![]() (Ⅲ)当BP=1时MP∥平面CNB1
(Ⅲ)当BP=1时MP∥平面CNB1
解析:
(Ⅰ)证明∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
∴BA,BC,BB1两两垂直.
以BA,BC,BB1分别为x,y,z轴建立空间直角坐标系,
则N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4)
∵![]() =(4,4,0)·(-4,4,0)=-16+16=0
=(4,4,0)·(-4,4,0)=-16+16=0
![]() =(4,4,0)·(0,0,4)=0
=(4,4,0)·(0,0,4)=0
∴BN⊥NB1, BN⊥B1C1且NB1与B1C1相交于B1, ![]()
∴BN⊥平面C1B1N; ……4分
(Ⅱ)设![]() =(x,y,z)为平面NCB1的一个法向量,
=(x,y,z)为平面NCB1的一个法向量,
则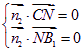
![]()
![]()
![]()
![]() ,取
,取![]() =(1,1,2),
=(1,1,2),
![]()
则cosθ=![]() ; ……9分
; ……9分
(Ⅲ)∵M(2,0,0).设P(0,0,a)为BC上一点,则![]() =(-2,0,a),∵MP∥平面CNB1,
=(-2,0,a),∵MP∥平面CNB1,
∴![]() ⊥
⊥![]()
![]()
![]() ·
·![]() =(-2,0,a) ·(1,1,2)=-2+2 a =0
=(-2,0,a) ·(1,1,2)=-2+2 a =0![]() a =1.
a =1.
又MP![]() 平面CNB1, ∴MP∥平面CNB1, ∴当BP=1时MP∥平面CNB1. …14分
平面CNB1, ∴MP∥平面CNB1, ∴当BP=1时MP∥平面CNB1. …14分

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目





