题目内容
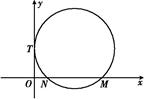
在平面直角坐标系xoy中,以点P为圆心的圆与圆x2+y2-2y=0外切且与x轴相切(两切点不重合).
(1)求动点P的轨迹方程;
(2)若直线mx一y+2m+5=0(m∈R)与点P的轨迹交于A、B两点,问:当m变化时,以线段AB为直径的圆是否会经过定点?若会,求出此定点;若不会,说明理由.
(1)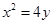 (
(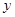 >
> );(2)会定点为
);(2)会定点为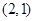 .
.
解析试题分析:本题主要考查两圆的位置关系、直线与抛物线的位置关系等数学知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,由于以点p为圆心的圆与x轴相切,通过数形结合得 且
且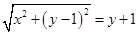 ,解出x与y的关系,即所求的P点的轨迹方程;第二问,直线与抛物线方程联立,消参得到关于x的方程,得到
,解出x与y的关系,即所求的P点的轨迹方程;第二问,直线与抛物线方程联立,消参得到关于x的方程,得到 ,
,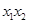 ,先写出以线段AB为直径的圆的方程,将
,先写出以线段AB为直径的圆的方程,将 ,
,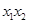 代入后,得到关于m的方程,由于m∈R,所以得到
代入后,得到关于m的方程,由于m∈R,所以得到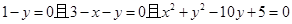 ,解出唯一解
,解出唯一解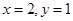 ,所以圆过定点(2,1).
,所以圆过定点(2,1).
试题解析:⑴设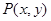 ,由题意知
,由题意知 且
且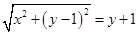 ,得
,得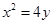
故所求点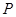 的轨迹方程为
的轨迹方程为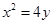 (
(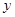 >
> ) 5分
) 5分
⑵设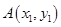 、
、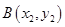 ,将
,将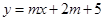 代入
代入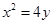 得
得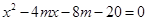
∴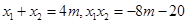 7分
7分
而以线段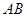 为直径的圆的方程为
为直径的圆的方程为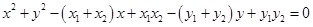 ,
,
即 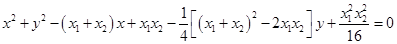 ,
,
得 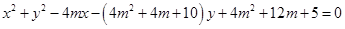 , 10分
, 10分
整理成关于 的方程
的方程 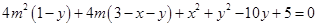
由于以上关于 的方程有无数解,故
的方程有无数解,故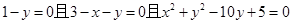 ,
,
由以上方程构成的方程组有唯一解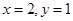 .
.
由此可知,以线段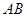 为直径的圆必经过定点
为直径的圆必经过定点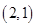 . 13分
. 13分
考点:1.抛物线的标准方程;2.直线与抛物线的位置关系;3.两个圆的位置关系.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 ,若椭圆
,若椭圆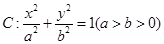 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为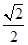 .
.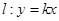 ,使得直线
,使得直线 与椭圆
与椭圆 分别交于
分别交于 两点,与圆
两点,与圆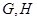 两点,点
两点,点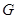 在线段
在线段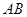 上,且
上,且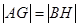 ,求圆
,求圆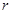 的取值范围.
的取值范围. =1(a>b>0),双曲线
=1(a>b>0),双曲线 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).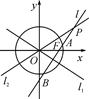
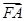 =λ
=λ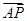 ,求λ的最大值.
,求λ的最大值.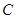 上任意一点
上任意一点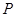 作直线
作直线 的垂线,垂足为
的垂线,垂足为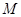 ,且
,且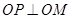 .
. 、
、 是曲线
是曲线 和
和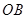 的倾斜角分别为
的倾斜角分别为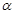 和
和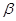 ,
,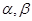 变化且
变化且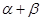 为定值
为定值 时,证明直线
时,证明直线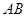 恒过定点,
恒过定点, =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=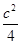 (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.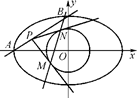
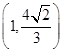 、
、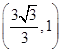 ,求椭圆C的方程;
,求椭圆C的方程;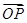 ·
·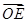 的值(O是坐标原点);
的值(O是坐标原点); =1的离心率为2,焦点到渐近线的距离等于
=1的离心率为2,焦点到渐近线的距离等于 ,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点. ,求直线l的方程.
,求直线l的方程. =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.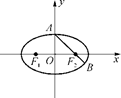
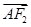 =2
=2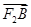 ,
,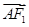 ·
· =
=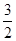 ,求椭圆的方程.
,求椭圆的方程. +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点( ,
, ).
).