题目内容
三个元件T1、T2、T3正常工作的概率分别为0.7、0.8、0.9,将它们的某两个并联再和第三个串联接入电路,如图甲、乙、丙所示,问哪一种接法使电路不发生故障的概率最大?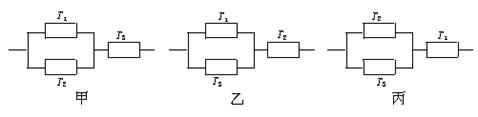

图甲的接法电路不发生故障的概率最大.
设元件T1、T2、T3能正常工作的事件为A1、A2、A3,电路不发生故障的事件为A,则P(A1)=0.7,P(A2)=0.8,P(A3)=0.9.
(1)按图甲的接法求P(A): A=(A1+A2)·A3,
由A1+A2与A3相互独立,则P(A)=P(A1+A2)·P(A3)
又P(A1+A2)=1–P(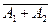 )=1–P(
)=1–P(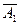 ·
·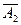 )
)
由A1与A2相互独立知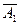 与
与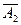 相互独立,得:
相互独立,得:
P(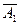 ·
·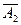 )=P(
)=P(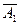 )·P(
)·P(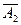 )=[1–P(A1)]·[1–P(A2)]
)=[1–P(A1)]·[1–P(A2)]
=(1–0.7)×(1–0.8)=0.06,∴P(A1+A2)=0.1–P(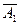 ·
·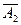 )=1–0.06=0.94,
)=1–0.06=0.94,
∴P(A)=0.94×0.9=0.846.
(2)按图乙的接法求P(A) A=(A1+A3)·A2且A1+A3与A2相互独立,则P(A)=P(A1+A3)·P(A2),
A=(A1+A3)·A2且A1+A3与A2相互独立,则P(A)=P(A1+A3)·P(A2),
用另一种算法求P(A1+A3).
∵A1与A3彼此不互斥,
根据容斥原理P(A1+A3)=P(A1)+P(A3)–P(A1A3),
∵A1与A3相互独立,
则P(A1·A3)=P(A1)·P(A3)=0.7×0.9=0.63,P(A1+A3)
=0.7+0.9–0.63=0.97
∴P(A)=P(A1+A3)·P(A2)=0.97×0.8=0.776.
(3)按图丙的接法求P(A),用第三种算法.
A=(A2+A3)A1=A2A1+A3A1,
∵A2A1与A3A1彼此不互斥,
据容斥原理,则P(A)=P(A1A2)+P(A1A3)–P(A1A2A3),
又由A1、A2、A3相互独立,得P(A1·A2)=P(A1)P(A2)=0.8×0.7=0.56,
P(A3A1)=P(A3)·P(A1)=0.9×0.7=0.63,
P(A1A2A3)=P(A1)·P(A2)·P(A3)=0.7×0.8×0.9=0.504,
∴P(A)=0.56+0.63–0.504=0.686.
综合(1)、(2)、(3)得,图甲、乙、丙三种接法电路不发生故障的概率值分别为0.846,0.776,0.686.故图甲的接法电路不发生故障的概率最大.
(1)按图甲的接法求P(A): A=(A1+A2)·A3,
由A1+A2与A3相互独立,则P(A)=P(A1+A2)·P(A3)
又P(A1+A2)=1–P(
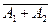 )=1–P(
)=1–P(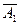 ·
·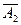 )
)由A1与A2相互独立知
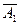 与
与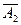 相互独立,得:
相互独立,得:P(
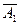 ·
·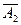 )=P(
)=P(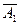 )·P(
)·P(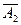 )=[1–P(A1)]·[1–P(A2)]
)=[1–P(A1)]·[1–P(A2)]=(1–0.7)×(1–0.8)=0.06,∴P(A1+A2)=0.1–P(
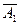 ·
·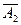 )=1–0.06=0.94,
)=1–0.06=0.94,∴P(A)=0.94×0.9=0.846.
(2)按图乙的接法求P(A)
 A=(A1+A3)·A2且A1+A3与A2相互独立,则P(A)=P(A1+A3)·P(A2),
A=(A1+A3)·A2且A1+A3与A2相互独立,则P(A)=P(A1+A3)·P(A2),用另一种算法求P(A1+A3).
∵A1与A3彼此不互斥,
根据容斥原理P(A1+A3)=P(A1)+P(A3)–P(A1A3),
∵A1与A3相互独立,
则P(A1·A3)=P(A1)·P(A3)=0.7×0.9=0.63,P(A1+A3)
=0.7+0.9–0.63=0.97

∴P(A)=P(A1+A3)·P(A2)=0.97×0.8=0.776.
(3)按图丙的接法求P(A),用第三种算法.
A=(A2+A3)A1=A2A1+A3A1,
∵A2A1与A3A1彼此不互斥,
据容斥原理,则P(A)=P(A1A2)+P(A1A3)–P(A1A2A3),
又由A1、A2、A3相互独立,得P(A1·A2)=P(A1)P(A2)=0.8×0.7=0.56,
P(A3A1)=P(A3)·P(A1)=0.9×0.7=0.63,
P(A1A2A3)=P(A1)·P(A2)·P(A3)=0.7×0.8×0.9=0.504,
∴P(A)=0.56+0.63–0.504=0.686.
综合(1)、(2)、(3)得,图甲、乙、丙三种接法电路不发生故障的概率值分别为0.846,0.776,0.686.故图甲的接法电路不发生故障的概率最大.

练习册系列答案
相关题目
 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为
 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、




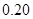






 人,至少有
人,至少有 人的日加工零件数落在区间
人的日加工零件数落在区间


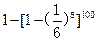

 ,反复这样投掷,数列
,反复这样投掷,数列 定义如下:
定义如下: ,若
,若 ,则事件“
,则事件“ ”的概率是( )
”的概率是( )


