题目内容
已知函数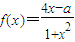 在区间[m,n]上为增函数,且f(m)f(n)=-4.
在区间[m,n]上为增函数,且f(m)f(n)=-4.(1)当a=3时,求m,n的值;
(2)当f(n)-f(m)最小时,
①求a的值;
②若P(x1,y1),Q(x2,y2)(a<x1<x2<n)是f(x)图象上的两点,且存在实数x使得
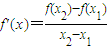 ,证明:x1<x<x2.
,证明:x1<x<x2.
【答案】分析:(1)已知函数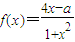 在区间[m,n]上为增函数,先用导数求得当a=3时的所有单调区间,则有[m,n]为函数f(x)单调区间的子集.
在区间[m,n]上为增函数,先用导数求得当a=3时的所有单调区间,则有[m,n]为函数f(x)单调区间的子集.
(2)①由 ,当且仅当f(n)=-f(m)=2时等号成立求解.
,当且仅当f(n)=-f(m)=2时等号成立求解.
②先分别表示出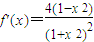 和
和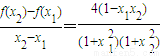 ,再由
,再由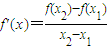 ,得到,
,得到,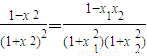 ,再用作差法比较
,再用作差法比较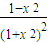 与
与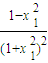 的大小.
的大小.
解答:解: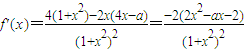 .(2分)
.(2分)
(1)当a=3时,由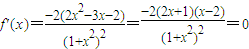 ,
,
得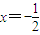 或x=2,
或x=2,
所以f(x)在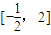 上为增函数,在
上为增函数,在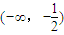 ,(2,+∞)上为减函数,(4分)
,(2,+∞)上为减函数,(4分)
由题意知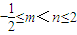 ,且
,且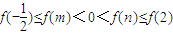 .
.
因为 ,所以
,所以 ,
,
可知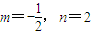 .(7分)
.(7分)
(2)①因为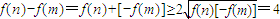 ,
,
当且仅当f(n)=-f(m)=2时等号成立.(8分)
由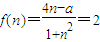 ,有-a=2(n-1)2≥0,得a≤0;(9分)
,有-a=2(n-1)2≥0,得a≤0;(9分)
由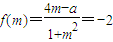 ,有a=2(m+1)2≥0,得a≥0;(10分)
,有a=2(m+1)2≥0,得a≥0;(10分)
故f(n)-f(m)取得最小值时,a=0,n=1.(11分)
②此时,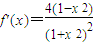 ,
,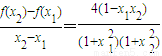 ,
,
由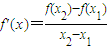 知,
知,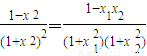 ,(12分)
,(12分)
欲证x1<x<x2,先比较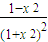 与
与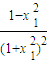 的大小.
的大小.
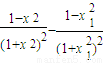
=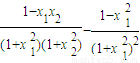
=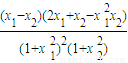
=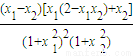
因为0<x1<x2<1,所以0<x1x2<1,有x1(2-x1x2)+x2>0,
于是(x1-x2)[x1(2-x1x2)+x2]<0,即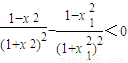 ,(13分)
,(13分)
另一方面,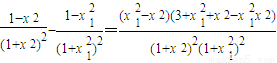 ,
,
因为0<x12x2<1,所以3+x12+x2-x12x2>0,从而x12-x2<0,即x1<|x|(14分)
同理可证x<x2,因此x1<|x|<x2.(15分)
点评:本题主要考查导数在研究单调性,求最值,比较大小中的应用.
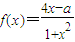 在区间[m,n]上为增函数,先用导数求得当a=3时的所有单调区间,则有[m,n]为函数f(x)单调区间的子集.
在区间[m,n]上为增函数,先用导数求得当a=3时的所有单调区间,则有[m,n]为函数f(x)单调区间的子集.(2)①由
 ,当且仅当f(n)=-f(m)=2时等号成立求解.
,当且仅当f(n)=-f(m)=2时等号成立求解.②先分别表示出
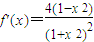 和
和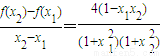 ,再由
,再由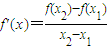 ,得到,
,得到,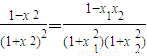 ,再用作差法比较
,再用作差法比较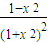 与
与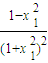 的大小.
的大小.解答:解:
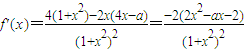 .(2分)
.(2分)(1)当a=3时,由
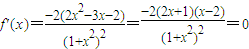 ,
,得
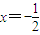 或x=2,
或x=2,所以f(x)在
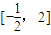 上为增函数,在
上为增函数,在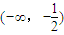 ,(2,+∞)上为减函数,(4分)
,(2,+∞)上为减函数,(4分)由题意知
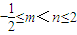 ,且
,且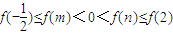 .
.因为
 ,所以
,所以 ,
,可知
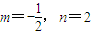 .(7分)
.(7分)(2)①因为
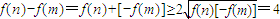 ,
,当且仅当f(n)=-f(m)=2时等号成立.(8分)
由
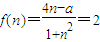 ,有-a=2(n-1)2≥0,得a≤0;(9分)
,有-a=2(n-1)2≥0,得a≤0;(9分)由
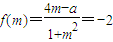 ,有a=2(m+1)2≥0,得a≥0;(10分)
,有a=2(m+1)2≥0,得a≥0;(10分)故f(n)-f(m)取得最小值时,a=0,n=1.(11分)
②此时,
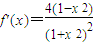 ,
,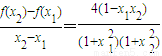 ,
,由
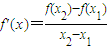 知,
知,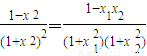 ,(12分)
,(12分)欲证x1<x<x2,先比较
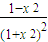 与
与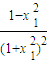 的大小.
的大小.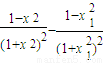
=
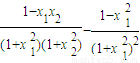
=
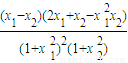
=
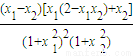
因为0<x1<x2<1,所以0<x1x2<1,有x1(2-x1x2)+x2>0,
于是(x1-x2)[x1(2-x1x2)+x2]<0,即
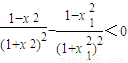 ,(13分)
,(13分)另一方面,
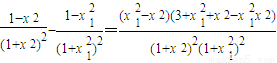 ,
,因为0<x12x2<1,所以3+x12+x2-x12x2>0,从而x12-x2<0,即x1<|x|(14分)
同理可证x<x2,因此x1<|x|<x2.(15分)
点评:本题主要考查导数在研究单调性,求最值,比较大小中的应用.

练习册系列答案
相关题目
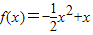 在区间[m,n]上的值域是[3m,3n],则m= n= .
在区间[m,n]上的值域是[3m,3n],则m= n= . 在区间M上的反函数是其本身,则M可以是( )
在区间M上的反函数是其本身,则M可以是( ) 在区间M上的反函数是其本身,则M可以是( )
在区间M上的反函数是其本身,则M可以是( )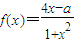 在区间[m,n]上为增函数,且f(m)f(n)=-4.
在区间[m,n]上为增函数,且f(m)f(n)=-4. ,证明:x1<x<x2.
,证明:x1<x<x2.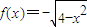 在区间M上的反函数是其本身,则M可以是( )
在区间M上的反函数是其本身,则M可以是( )