题目内容
[番茄花园1] 以知椭圆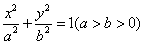 的两个焦点分别为
的两个焦点分别为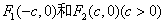 ,过点
,过点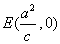 的直线与椭圆相交与
的直线与椭圆相交与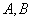 两点,且
两点,且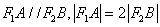 。
。
(1)求椭圆的离心率;
(2)求直线AB的斜率;
(3)设点C与点A关于坐标原点对称,直线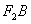 上有一点
上有一点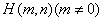 在
在
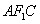 的外接圆上,求
的外接圆上,求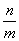 的值。
的值。
[番茄花园1]26.
[番茄花园1] 解:(1)由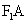 //
//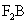 且
且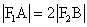 ,得
,得 ,从而
,从而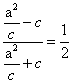
整理,得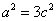 ,故离心率
,故离心率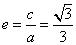
(2)解:由(1)得 ,所以椭圆的方程可写为
,所以椭圆的方程可写为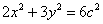
设直线AB的方程为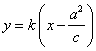 ,即
,即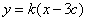 .
.
由已知设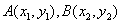 ,则它们的坐标满足方程组
,则它们的坐标满足方程组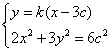
消去y整理,得
依题意,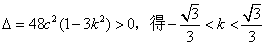
而
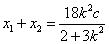 ①
①
 ②
②
由题设知,点B为线段AE的中点,所以
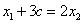 ③
③
联立①③解得
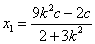 ,
,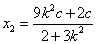
将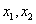 代入②中,解得
代入②中,解得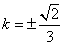 .
.
(3)解法一:由(II)可知
当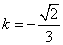 时,得
时,得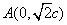 ,由已知得
,由已知得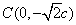 .
.
线段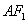 的垂直平分线
的垂直平分线 的方程为
的方程为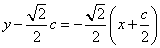 直线
直线 与x轴的交点
与x轴的交点
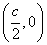 是
是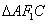 外接圆的圆心,因此外接圆的方程为
外接圆的圆心,因此外接圆的方程为 .
.
直线 的方程为
的方程为 ,于是点H(m,n)的坐标满足方程组
,于是点H(m,n)的坐标满足方程组
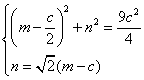 , 由
, 由 解得
解得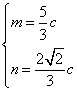 故
故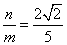
当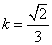 时,同理可得
时,同理可得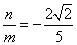 .
.
解法二:由(II)可知
当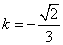 时,得
时,得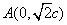 ,由已知得
,由已知得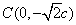
由椭圆的对称性可知B,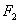 ,C三点共线,因为点H(m,n)在
,C三点共线,因为点H(m,n)在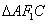 的外接圆上,
的外接圆上,
且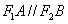 ,所以四边形
,所以四边形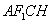 为等腰梯形.
为等腰梯形.
由直线 的方程为
的方程为 ,知点H的坐标为
,知点H的坐标为 .
.
因为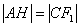 ,所以
,所以 ,解得m=c(舍),或
,解得m=c(舍),或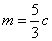 .
.
则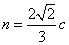 ,所以
,所以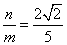 .
.
当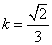 时,同理可得
时,同理可得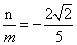
[番茄花园1]26.

[番茄花园1] 已知m是非零实数,抛物线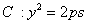 (p>0)
(p>0)
的焦点F在直线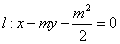 上。
上。
(I)若m=2,求抛物线C的方程
(II)设直线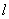 与抛物线C交于A、B,△A
与抛物线C交于A、B,△A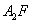 ,△
,△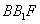 的重心分别为G,H
的重心分别为G,H
求证:对任意非零实数m,抛物线C的准线与x轴的焦点在以线段GH为直径的圆外。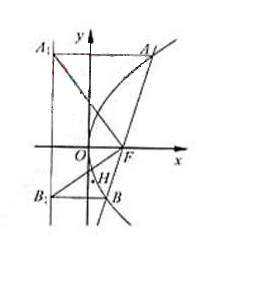
[番茄花园1]1.
[番茄花园1] 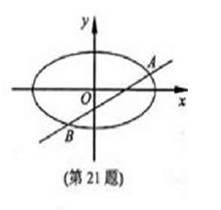 已知m>1,直线
已知m>1,直线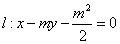 ,
,
椭圆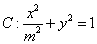 ,
,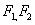 分别为椭圆
分别为椭圆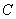 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线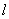 过右焦点
过右焦点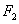 时,求直线
时,求直线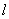 的方程;
的方程;
(Ⅱ)设直线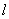 与椭圆
与椭圆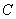 交于
交于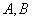 两点,
两点,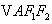 ,
,
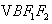 的重心分别为
的重心分别为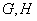 .若原点
.若原点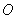 在以线段
在以线段
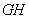 为直径的圆内,求实数
为直径的圆内,求实数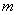 的取值范围.
的取值范围.
[番茄花园1]1.
 ),两个焦点为(—1,0)(1,0)。
),两个焦点为(—1,0)(1,0)。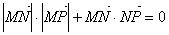
 与曲线C交于A、B两点,那么在曲线C上是否存
与曲线C交于A、B两点,那么在曲线C上是否存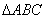 是以AB为斜边的直角三角形?若存在,求出m的取值范围;若不存在,
是以AB为斜边的直角三角形?若存在,求出m的取值范围;若不存在,